
Table of Contents
- Teaching Geometry during the Pandemic by Pat Herbst
- GeT Activity: Looking for Intersections between Geometry and Art by Gloriana Gonzáles & Christine Rinkenberger
- Contributed Essay: When More is Not Always Better: On How NOT to Approach an Elementary Construction Problem by Eisso J. Atzema
- GeT to Know the Community: Steven Boyce
- Reporting on the MKT-G Results from GeT Students by Mike Ion
- Recent Publications

Teaching Geometry during the Pandemic
by Pat Herbst
Here we are with GeT: The News! It’s May of 2020, and what’s new? Since the last Newsletter, COVID-19 has brought challenges and changes to everybody in the world, including those of us in higher education. Lives have been lost to COVID-19, including those whose work was close to the work of our community. Among them was Judah Schwartz, who (with Michal Yerushalmy) created The Geometric Supposer, the first in a genre of applications that are now described generically as dynamic geometry software. This terrible disease has touched every one of us in one way or another. Our thoughts are with those who have lost loved ones.
Even for those of us who have not suffered physically, our lives have been disrupted in countless ways. As I write this, I know some of you are finishing grading courses that started face to face and ended online, while others have recently started teaching classes that they know will be completely online. We look into the Fall with uncertainty as to whether classes will or will not meet on our campuses. I imagine that most of us have been trying to cope with this new reality and that in most cases any desire to innovate has been put momentarily to the side. I also imagine that, in teaching as in many other aspects of our lives, once the pandemic hopefully begins to recede we will start reflecting on what we have learned from the experience. I wonder if the experiences of teaching online during the COVID-19 pandemic will elicit both problems and ideas that could have an impact on the teaching of geometry for future teachers in the long term.
One idea that we have been considering is using video annotation as a way to structure students’ activity online. Suppose, for example, that you had a video of students discussing the solution to the question, “we know that the angle bisectors of a triangle meet at a point, but what about a quadrilateral?” As one can appreciate, the question is not very clearly stated, which suggests that a discussion of it might include figuring out what mathematical question would be worth asking. The question could be “do the angle bisectors of a quadrilateral meet at a point?”; “on what conditions do the angle bisectors of a quadrilateral meet at a point?”; or perhaps “how could we describe the intersection of the angle bisectors of a quadrilateral?” Would it be useful to you to have your students view and comment on a video that presented a discussion of how to make that question more precise? What goals would you have? How would making comments on such a video prepare your students to pose and solve geometric problems themselves or to teach geometry?
Several years ago we developed a set of animations of classroom scenarios, many of which were situated in high school geometry classrooms and represented how a class might approach a geometry problem. Our goal was not to show exemplary instruction but rather to depict things that could happen in classrooms; we were using those animations as triggers for discussions among high school teachers. One of these scenarios, The Square, started with the teacher presenting the question cited above. A student immediately came to the board and drew a square and its diagonals, claiming that they met at a point. A second student said that if one just extended a pair of parallel sides in the square they could see that the angle bisectors and the diagonals were not the same things. At the insistence of the first student that his claim was only about the square, the class spent some time showing that the diagonals of a square bisect its angles. The discussion was, of course, much more lively and messy than how I am describing it. But, hopefully, my rendition will pique your curiosity and you will be interested in seeing it. You can find it online here.
Some years after we created that animation, our colleague Emina Alibegovic (now teaching in Salt Lake City) was teaching geometry for teachers in the mathematics department at Michigan. Emina decided to show the animation to her students and asked them to tap their desks whenever they saw students doing a mathematical action. The latter expression is rather ill-defined, and purposefully so—it was up to the students to recognize what might be mathematical in the story: a restatement of the question, the assignment of notation, a claim, an argument, a counterexample, etc. After Emina’s students brought up a variety of mathematical issues from the animation, they touched on precision questions (e.g., can one really say that the diagonals and the angle bisectors are the same in the square?), and spent much of the time figuring out whether the proof offered was valid and what was the statement that the proof proved. Watching that discussion in Emina’s class made me think that the animations could be used to teach mathematics to teachers: The animation could immerse future teachers not only in the classroom context, but also in the mathematical content that they needed to learn in order to be able to teach in the future.
Fast forward a few years and now we also have developed a piece of software, Anotemos (www.anotemos.com), that allows users to collaboratively annotate videos. I wonder whether a task similar to what Emina posed to her class could be done online using Anotemos. The advantage of doing it online and mediated by software is that annotations can be done asynchronously: students can play and annotate the video at their own leisure. Anotemos also has a lot of functionalities, not only to enable users to attach comments to moments in the timeline but also to places on the video screen; it also allows instructors to decide when the users can see each others’ comments. If this is something you might be interested in trying in your GeT course in the Fall, we’d be very interested in supporting you. Please be in touch!
Our next newsletter will come out in the Fall. I can’t begin to imagine what the world and higher education will look like then, but I hope that our GeT: A Pencil community can continue to support you no matter what form your courses take. Until then, best wishes for the health and safety of you and your loved ones.

GeT Activity: Looking for Intersections between Geometry and Art
by Gloriana González and Christine Rinkenberger
Motivated by the goal of engaging more students in doing mathematics, we have been investigating connections between geometry and art. Geometry textbooks include problems that are situated in various art-based contexts such as architecture, crafts, and drawing. In our conversations with geometry teachers, we have found that they welcome opportunities to teach geometry through art. Nevertheless, they ponder how to find artbased contexts that are relevant for their students.
Origami is one way to incorporate art into mathematics lessons. Origami is not only engaging, but useful and beautiful. Aerospace engineers design artifacts based on origami principles to efficiently package them. Architects have been inspired by origami to design beautiful buildings. Fashion designers have turned to origami to create original designs. By opening connections between the art of paper folding, which is practiced in various cultures, and geometry, we can promote students’ deep engagement with mathematics.
When we worked with focus groups with high school geometry teachers, they said that origami can increase students’ engagement. One teacher said, “I like the origami [crane problem], just because [students] get to manipulate it and actually look at those things.” Another teacher said that students have seen origami before, even if they had not made origami pieces, so they can build on their previous knowledge.
Here, we share two activities for teaching congruence criteria for triangles through origami. We take advantage of folding to promote students’ identification of figures with reflection symmetry. The problems exemplify how to use transformation geometry in relation to the definition of congruence.
Christine’s Origami Heart Activity
In my Geometry classroom, I wanted to bridge the prior unit’s construction work to the current unit’s triangle congruence. During the construction unit, students who were normally discouraged became really engaged with the hands-on aspect of the work. I liked the idea of using origami to build on that engagement. In addition, I wanted to elicit students’ prior knowledge about transformations, which we had learned in our first unit. The students followed my modeling and a video to create an origami heart (Figure 1). I then asked them to unfold their origami heart and answer the following questions:
- What lines of symmetry do you see? Highlight three of them.
- What transformations do you see on your paper?
- Are there congruent figures on your paper?

After giving the students time to consider these questions individually, we had a class discussion and began to tie in the mathematical vocabulary, such as the term rigid, that we had used previously. It led into the idea that if a rigid transformation occurs, then the pre-image and the image will be congruent. That was the objective of our following lesson and the foundation of the congruence unit. While this lesson was meant to be an introductory activity, it could be extended into a longer learning task.
The Origami Crane Problem
Another problem uses an origami crane to study the properties of congruent triangles (Figure 2). After demonstrating how to create the crane, instruct students to open the square origami paper to study the crease patterns (Figure 3). Point out that there are many symmetric patterns that appear interesting, but it is unclear how they were created. Ask them to work in pairs to answer the following questions:
- Use color pencils to identify as many pairs of congruent angles as possible
- Choose a pair of congruent triangles and prove that they are congruent.
- Find two figures that are reflections of one another. Explain how you know that they are a reflection.
- Talk to another pair about number 3. Do you agree with their explanation? Why or why not?
Another related activity involves reproducing the “opened” origami crane using GeoGebra (Figure 4). Students could use dynamic geometry and discuss various ways to construct it, including constructions by using reflections. Students could also create art with the diagram as in Figure 5.


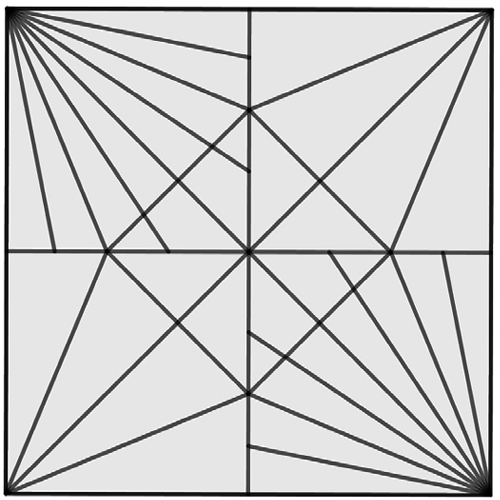
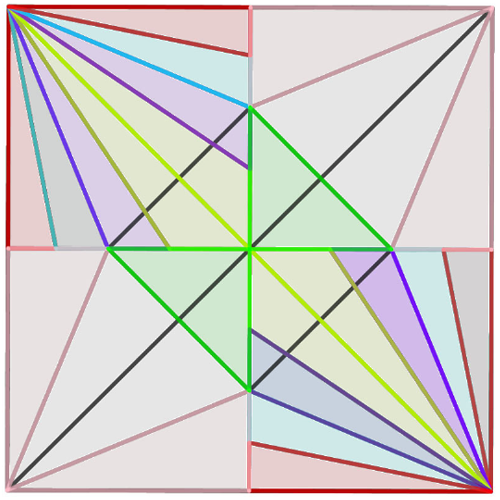
Overall, the teachers we worked with anticipated that origami-based problems could provide opportunities to connect with properties of reflections, and they valued that students could share different things that they noticed about the creases.
Gloriana González is Associate Professor of Mathematics Education at the University of Illinois at Urbana-Champaign. Christine Rinkenberger is an alumna of UIUC and works at the Urbana School District.

Contributed Essay: When More is Not Always Better: On How NOT to Approach an Elementary Construction Problem
by Eisso J. Atzema
Introduction
When the Danish mathematics professor Julius Petersen (1839-1910) published Metoder og teorier til løsning af geometriske konstruktionsopgaver (Methods and Theories for the Solution of Problems of Geometrical Constructions, Petersen, 1866), his handbook on geometrical constructions initially did not draw much attention. However, when a second addition appeared in 1879, it was translated into at least seven other languages within the next four years (for English, see Petersen, 1879). Ever since, the book has been considered a classic among aficionados of construction problems in Euclidean geometry. Part of the appeal of the book is a set of 400+ problems of increasing difficulty with often extremely succinct solutions. To this day, it is not uncommon to find geometry lovers musing on the kind of solution Petersen may have envisioned to one of his problems. A case in point is the Brazilian-Canadian math educator Luís Lopes, who recently appealed for help with a reconstruction of Petersen’s solution to Problem 327: “Construct a triangle, which shall have its vertex in a given line, having a given base and a given difference of the angles at the base” (see Lopes, 2020; Petersen, 1879, p.59).
A First Solution
When I first saw Luís’ message, I did not think the problem was a hard one. In fact, let AB be the given line segment and let ℓ be the given line. Now, let C be any point in the plane such that ∠BAC exceeds ∠ABC by a fixed angle. If we assume these angles to be oriented, this angle condition defines a projective relation between the pencil of lines centered at A and the pencil centered at B. For any such relation, the locus of all points of intersection of corresponding lines is a conic section C. Therefore, the vertex C of any solution triangle ABC has to lie on C as well as on ℓ. However, there were a few issues with this solution. First of all, since ℓ and C generally meet in two points, which point is the right C? Could there perhaps be two solutions to Problem 327? In fact, might it be that ℓ and C do not meet at all, in which case there would not be a solution to Problem 327? More importantly, clearly this was not the kind of solution that Petersen had in mind. All of his construction problems are elementary, in that they can be solved with the use of ruler and compass only.
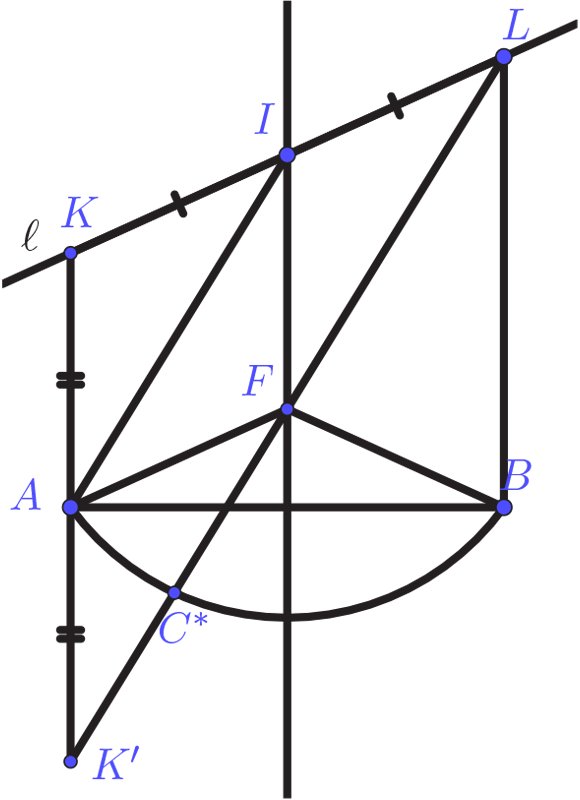
After some thought, I found a way to overcome the last issue (see Figure 1). Note that without loss of generality we may assume that all solution triangles ABC are oriented in the same way. In other words, we may assume that all candidates for C lie on the same side of the line AB. In fact, to find a solution with opposite orientation, we just reflect ℓ in AB, solve the problem for that configuration and reflect the solution triangle in AB again. Thus, with A to the left of B, we may assume that C lies “above” the line segment AB, i.e. on the same side of AB as the top of the page. Now, let C be such that ∠BAC exceeds ∠ABC by a fixed angle γ and that C∗ on AC is such that BC∗ is the reflection of BC in AB. Then, by construction, ∠AC∗B equals γ. That is, C∗ lies on a circular arc ΣAB. Conversely, any point on ΣAB comes from a point C such that ∠BAC exceeds ∠ABC by γ. Next, note that the procedure mapping C to C∗ defines a transformation π on the whole plane. Therefore, the points of intersection of C with ℓ that we are interested in now correspond to the points of intersection of ΣAB with ℓ∗ = π(ℓ). What is more, since it can be shown that π is projective, ℓ∗ is a straight line as well. By construction, if K and L on ℓ are such that KA ⊥ AB and LB ⊥ AB, ℓ∗ passes through L and K′ , the reflection in AB of K. Therefore, we can now easily find the point(s) of intersection of ℓ∗ with ΣAB. Finally, let C∗ be such a point of intersection. Then, the corresponding point C is just the point of intersection of ℓ with the line C∗A. In other words, we now have a way of constructing C by means of ruler and compass only. Unlike my previous solution, this approach provides some insight into the number of solutions to Petersen’s problem. Clearly, if the line ℓ is such that both K and L lie “above” AB, there is only one solution to Problem 327. Given that C is assumed to lie above AB, the same is true in case K and L lie on opposite sides of the line segment AB. This only leaves the solution to the case that K and L both lie below AB unclear (an issue that the scope of this note does not allow us to explore). Still, even though the construction is elementary, its derivation is not. All in all, it seemed unlikely that this was the solution of Problem 327 that Petersen had in mind and it was no surprise that Luís did not care much for my construction.
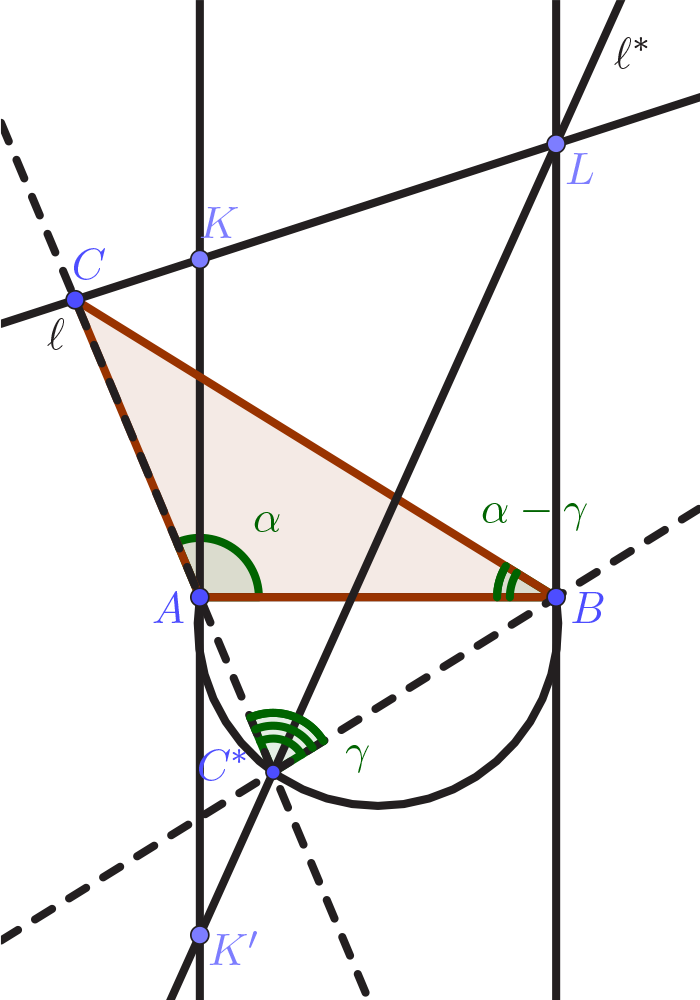
A More Elementary Approach
As it turned out, Petersen’s problem comes with a hint. In fact, he suggests to switch the end points of the given line segment (possibly referring to a reflection) and then to use the “method of similitude” (basically the notion that non-congruent figures can be obtained from one another by means of a single dilation if and only if they are directly similar and similarly situated). With this in mind, it is not much of a leap to a more “natural” solution to Problem 327. The idea is as follows (see Figure 2)
Let ABC with C on ℓ be a solution to Problem 327. Now, let m be the reflection of ℓ in the perpendicular bisector of AB and let D be the reflection of C in the same line. Then ABCD is an isosceles trapezoid and both ∠CAD and ∠CBD equal the fixed angle γ. Thus, A and B lie on a circular arc ΣCD that is directly similar to the arc ΣAB defined above. Now, let C′ and D′ be any two points on ℓ and m respectively such that C′ D′ is parallel to CD and let δ be the dilation centered at I = ℓ ∩ m such C′ = δ(C), D′ = δ(D), and ΣC′D′ = δ(ΣCD). By construction, A′ = δ(A)=ΣC′D′ ∩ IA and B′ = δ(B)=ΣC′D′ ∩ IB. But that means that we can construct A′ and B′ such that A′ B′ C′ is similar to the triangle ABC we are looking for. All that is left to do is to construct ABC as a triangle on AB that is directly similar to the triangle A′B′C′ . Alternatively, we can construct C as the point of intersection of ℓ with the line through A and parallel to A′C′.
Reconciling the Two Solutions
The preceding construction appears to take Petersen’s hints into account and I think Luís was perfectly happy with this solution. To me, however, the whole procedure remained somewhat unsatisfactory in that it is not fully deterministic: even though the outcome is completely determined by our choice of ℓ and AB, the intermediate steps are not. So, what if my earlier elementary construction could be derived from this second elementary construction? Actually, this is not too hard to do (see Figure 3). Indeed, if we retain all notations of Figure 2, K′L is by construction parallel to IA and has twice its length. Now, let F be the point of intersection of K′L with the perpendicular bisector of AB. Since I is the midpoint of KL and IF is parallel to KK′ , it follows that F is the midpoint of K′L. Therefore, since A is the midpoint of KK′ , AF is parallel to ℓ. By a similar argument, BF is parallel to m. Since C′D′ (in Figure 2) and AB are by construction parallel as well, there is a dilation δ′ that transforms ABF into C′D′I by Petersen’s Method of Similitude. As before, let C∗ = ΣAB ∩ K′L. Since ΣAB is similar to ΣC′D′ and the lines K′L and IA are parallel, it follows that δ (ΣAB)=ΣC′D′ and δ′ (K′ L) = IA. Consequently, δ′ (C∗) = δ′ (ΣAB ∩ K′ L) = δ′ (ΣAB) ∩ δ′ (K′ L) = ΣC′D′ ∩IA, which is A′ in Figure 2. We conclude that C∗A and C′A′ = δ′(C∗A) are parallel, which proves that the first elementary construction always leads to the same result as the second.
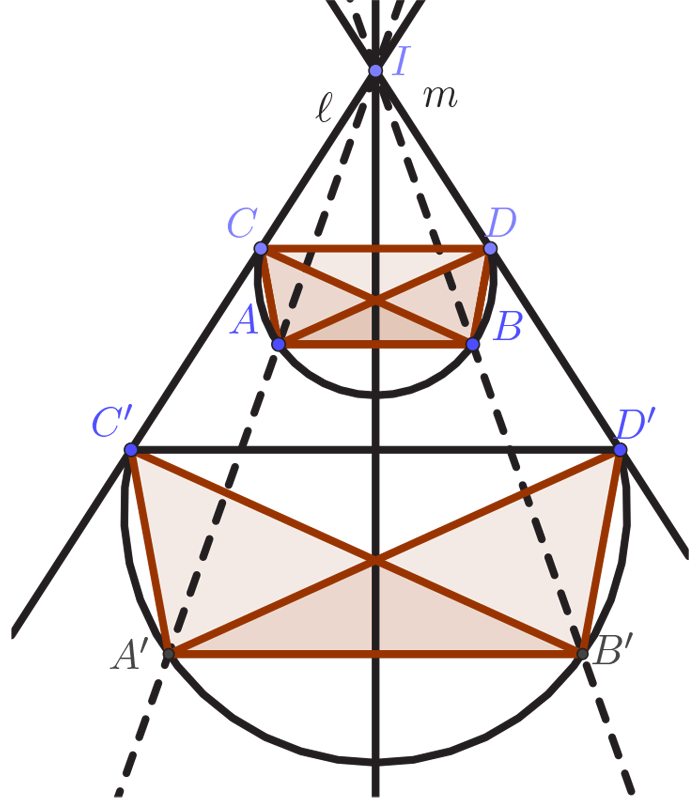
Final Thoughts
Thus, we have a deterministic construction for Petersen’s Problem 327 for which we also have an elementary derivation. Nonetheless, is this construction really a “better” or more “elegant” solution than what Petersen probably had in mind? More importantly, in any teaching context, would the extra effort to get to the deterministic solution really be justifiable? It was a fun exercise to bring my original, more advanced approach down to the more elementary level that Petersen envisioned. On balance, however, I feel that Peterson’s own approach has more of a natural flow to it and that bringing in more advanced mathematics was just not the right way to go. On the other hand, verification that my initial elementary construction always gives a solution to Problem 327 might make for a good classroom problem. Of course, there is also the issue of what exactly happens when ℓ lies “below” AB.
Eisso J. Atzema is a Lecturer at the University of Maine.
References
Lopes, Luís (January 20, 2020). Re: Triangle construction [electronic list message]. Retrieved from: groups.io/g/euclid/message/546
Petersen, Julius (1866). Metoder og teorier til løsning af geometriske konstruktionsopgaver (…). Copenhagen:Schønberg.
Petersen, Julius (1879). Methods and Theories for the Solution of Problems of Geometrical Constructions (…). Copenhagen: Andr. Fred. Høst & Son. (also accessible on Google Books)

GeT to know the community
Four questions with Steven Boyce, Assistant Professor of Mathematics and Statistics at Portland State University
- What is special about your GeT course? I am a former high school geometry teacher, so I include my perspective of what was useful and what was missing from my own preparation in college for teaching high school geometry in my GeT course. My course begins with finite geometry, then transitions to Euclidean for the majority of the course, and closes with taxicab, hyperbolic, and spherical geometries. We use Geogebra quite often, and I previously had students collaborating with groupmates on classwork by uploading snapshots to the LMS or typing into a Google Doc; this helped with the transition to remote teaching, as I give students the choice of participating synchronously or asynchronously.
- Who are your students? Most of my students are undergraduates and either math majors or math minors. About half the students are prospective secondary math teachers. There are typically a few post-baccalaureate students in the class, as it is a requirement for entry into the teaching program that students are often missing if they didn’t focus on preparing to become a teacher as an undergraduate. There are students of a variety of ages and backgrounds in my classes, which provides (mostly) benefits but also some challenges.
- What are you most interested in learning/achieving through participating with the GeT: A Pencil community? I’m grateful for the opportunity to learn about the variety of emphases that colleagues across the country have had in their courses. I haven’t been able to participate as much this quarter with the demands of remote teaching, but I am excited about the products coming out of both of the Working Groups and feel fortunate that I was able to contribute my ideas.

- What is your favorite book you have read recently? With the current sheltering-in-place, I recommend the dystopian Children of Men, by P. D. James. It’s been about 10 years since I’ve read it and am itching to read it again. My favorite academic book I’ve re-read recently is probably von Glasersfeld’s Radical Constructivism, which, for me, is also a great pleasure to read.
Did you get promoted? Win a grant? Have a baby? Buy a house? We would love to feature your news, whether professional or personal! Email us at GRIP@umich.edu.

Reporting on the MKT-G Results from GeT Students
by Mike Ion
In this article, I share what the GRIP Lab has learned by collecting responses from Geometry for Teachers (GeT) students who have taken our mathematical knowledge for teaching geometry (MKT-G) assessment before and after taking the GeT course.
MKT-G instrument
Herbst and Kosko (2014) developed an instrument to measure MKT-G that follows the definitions of content knowledge for teaching from Ball, Thames, and Phelps (2008). We used that instrument to estimate preservice teachers’ MKT-G using a unidimensional item response theory (IRT) model.
To understand the participating GeT students’ MKT-G growth in relation to inservice teachers’ MKT-G, GeT students’ MKT-G scores were estimated using a distribution of in-service teachers’ MKT-G scores. Specifically, GeT students’ item responses were aggregated with the responses to the same 21 stem items by 605 in-service teachers so that GeT students’ MKT-G standing relative to the in-service teachers could be examined.
Research Questions
- What is the growth in MKT-G scores that happens during a GeT course?
- How do GeT students compare in MKT-G to a national sample of inservice teachers?
- Are there differences in the growth of MKT-G scores between students who seek teaching certification and other students also taking the GeT course?
Data
This analysis considers the responses from 222 students taking 15 GeT courses taught by 13 GeT instructors in the 2018/2019 academic year. Of these 222 students, 123 (55.4%) of them were preparing for teacher certification.
Method
We estimate the growth in MKT-G scores using a linear regression model:
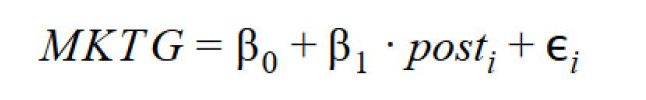
where β0 is the average MKT-G IRT score at the beginning of the semester and is the estimated growth in MKT-G IRT scores at the end of the semester. This regression model is equivalent to a paired t-test that compares the average MKT-G IRT scores before and after the Geometry for Teachers course. Using a regression allows us to adjust the growth estimate for students’ covariates. We adjust our estimates for students’ programs and majors as well as students’ demographic characteristics.
Results/Discussion
Three main results emerge: (1) On average, students score about 0.161 standard deviation units higher on the MKT-G test after completing the Geometry for Teachers course, after controlling for student programs and majors, and their demographic characteristics. (2) Students taking the MKT-G test score about one standard deviation below inservice teachers (with an average of 14.2 years of mathematics teaching) that took the same test, on average. (3) Students who plan to be mathematics teachers have higher gains in MKT-G than other students, on average (.234 standard deviation growth compared to .09). These results highlight some main conclusions about the Geometry for Teachers course. First, teachers develop knowledge about geometry while they teach. The difference between the students in our sample and the average inservice teacher is about the expected growth in teacher knowledge that happens after teaching geometry for five years (see Desimone, Hochberg, & McMaken, 2016). Second, taking a specialized GeT course appears to close this gap in knowledge by about one year. As we move forward with this work, we gain understandings of the importance and value of the GeT course for preservice teachers
Mike Ion is a Research Assistant in the GRIP Lab.
References
Ball, D., Thames, M. H., & Phelps, G. (2008). Content knowledge for teaching: What makes it special? Journal of Teacher Education, 59(5), 389–407.
Desimone, L., Hochberg, E. D., & McMaken, J. (2016). Teacher knowledge and instructional quality of beginning teachers: Growth and linkages. Teachers College Record, 118(5), 1–54.
Herbst, P., & Kosko, K. (2014). Mathematical knowledge for teaching and its specificity to high school geometry instruction. In J.-J. Lo, K. R. Leatham, and L. R. Van Zoest (Eds.), Research trends in mathematics teacher education (pp. 23–45). Cham: Springer.

Recent Publications
Herbst, P., Ko, I., & Milewski, A. (in press, online first). A heuristic approach to assess change in mathematical knowledge for teaching geometry after a practice-based professional learning intervention. Published online at Research in Mathematics Education. doi: 10.1080/14794802.2019.1704851
To submit a paper to be highlighted in a future newsletter, please fill out this form.
GeT Support
Sponsored by NSF DUE-1725837. All opinions are those of the authors and do not necessarily represent the views of the National Science Foundation or the University of Michigan.
Patricio Herbst, PI
Amanda Milewski, Co-PI
Erin Lichtenstein, Get: The News Editor
Get Support is housed in the GRIP Lab at the University of Michigan
Inese Berzina Pitcher, Project Manager
