GeT: The News! Volume 6, Issue 2, Spring 2025

Table of Contents

• Opening Note by Stephen Szydlik
• Rediscovering the value of Euclid’s Elements by Maureen T. Carroll and Elyn Rykken
• Practices Empower our Students by Jason Belnap and Amy Parrott
• Working Group Updates
• GeT to Know the Community: Henry Escuadro
• Closing Note by Steve Boyce and Stephen Szydlik

Opening Note

by Stephen Szydlik

The GeT News editorial team is excited to share the latest news and developments from our vibrant GeT community. This issue highlights the continued thoughtful work being done to deepen geometry instruction for future teachers.  We feature two articles drawn from the forthcoming GeT Support book: a description of a GeT course built around Euclid’s Elements, and an essay encouraging GeT instructors to identify and develop “micro-practices” through a cycle of inquiry with their students. We also include updates from our working groups and an interview with long-time GeT community member Henry Escuadro.

As another academic year winds down, it has become impossible to ignore the current challenges facing higher education. I have just completed my 29th year as a university faculty member, and while I sometimes still feel like a rookie instructor, the gray hair identifies my senior status.  During my years as a teacher, I’ve observed up and down cycles in the fortunes of academia, but I’ve never seen anything like the headwinds we currently face.  In the last two years at my own institution, I’ve witnessed ongoing enrollment and retention struggles, program and staff cuts, the continued loss of public support (both financial and otherwise), student engagement and mental health difficulties, and vocal attacks by politicians.  During these challenging times, the GeT community continues to be a source of strength and inspiration.   Whether you’re a “senior” like me or new to the GeT community, here you will find a group of committed and supportive educators working together to effect positive change.  And whether you’re exploring ways to model geometric reasoning, revisiting classical foundations, or refining your own pedagogical practices, we hope the reflections and resources in this issue offer you both insight and inspiration.

Suggested Citation

Szydlik, S. (2025, June). Opening Note. GeT: The News!, (6)2. https://www.gripumich.org/v6-i2-sp2025/#opening-note

Rediscovering the value of Euclid’s Elements

by Maureen T. Carroll, University of Scranton and Elyn Rykken, Muhlenberg College

Written over 2000 years ago, The Elements is an achievement of historical significance, possessing a clarity, rigor and superior organization that set the standard for the axiomatic development of every field of study. No other mathematics book has been published as many times or read by as many people, spanning multiple millennia, continents and languages. In our chapter of the forthcoming GeT volume we describe how we use Euclid’s masterpiece as the scaffolding for a course designed for future educators that dovetails nicely with the GeT SLOs.

Composed of thirteen books of axioms, definitions, propositions and their proofs, Euclid’s words are familiar, yet unexplored, and the axiomatic structure offers a well-defined entry-level experience. Euclid’s proofs are verbose and lack much of the symbolic language and notation we have come to expect, providing a rare opportunity in the curriculum to recognize the underappreciated brevity and clarity of algebraic notation as a ‘technological invention.’ As Bach’s experience of transcribing the string pieces of Vivaldi for the organ was transformative for the young composer’s skills, we flip the classroom and give students hands-on practice as they present and explain the proofs to their peers. In doing so, they transcribe Euclid’s wordy proofs into a more economical mixture of words, symbols and notation to develop the skills necessary to evaluate geometric arguments and understand the relationship between definitions, axioms and theorems. Students present most of the Book I propositions in class, but some constructions and justifications are completed with GeoGebra using our book of lab projects as their guide.

With a solid foundation of Neutral geometry established by the halfway point of Book I, our path takes a detour to reconsider our preconceived notions of line, circle and straightness. Here we use hands-on workshops to explore Euclidean axioms and propositions within the context of spherical and taxicab geometries. These side trips reveal flaws in Euclid’s reasoning and open the door to a discussion of models as well as desirable properties of axiomatic systems. After dipping our toes in non-Euclidean waters, we return to the non-Neutral second half of Book I to work through the propositions on parallels and comparative area that ultimately culminate in the Pythagorean Theorem and its converse. A careful study of the masterful development of Book I is an ideal way to develop deep roots in this geometry, and furthermore, provides an opportunity to shine a light on the chasm that existed between algebra and geometry for nearly two millennia.

After touring through Euclid’s geometry of the plane with selections from Books II, III and IV, we turn to the dramatic resolution of centuries of attempts to prove the Parallel Postulate. With a firm footing in Euclidean geometry, students have the tools needed to tackle hyperbolic, finite and transformational geometries as well as the four impossible constructions from antiquity. Along our curated path, the transitions to and away from The Elements are designed to push the narrative forward while consistently reinforcing the fundamentals and seamlessly interlacing the stories of the mathematicians who give life to the rich history of geometry. We find that this path offers a compelling and coherent narrative for our students to follow while providing essential resources for our future educators to utilize as they enter their own classrooms.

Suggested Citation

Carroll, M., and Rykken, E. (2025, May). Rediscovering the value of Euclid’s Elements. GeT: The News!, (6)2. https://www.gripumich.org/v6-i2-sp2025/#rediscovering-the-value-of-euclids-elements

Practices Empower our Students

by Jason Belnap, University of Wisconsin – Oshkosh and Amy Parrott, University of Wisconsin – Oshkosh

K-12 teachers shape the public view of mathematics.  They are the first representatives of the math community.  If we want the public and our future students to understand what math is really like, we need teachers who have acquired mathematical practices: habits, values, and characteristics that enable them to independently generate and access mathematical knowledge, reason and communicate mathematically, and create authentic mathematical experiences for their students. Thus, in teaching preservice teachers, we feel it imperative that we focus our teaching on helping them develop mathematical practices, some of which are found in the SLOs, such as: making sense of problems and persevering in solving them (e.g. SLO 2 & SLO 10), generating and utilizing mathematical representations (e.g. SLO 6 & SLO 8), reasoning mathematically and constructing viable arguments (e.g. SLO 1 & SLO 5), communicating mathematical ideas through the precise use of language and symbols (e.g. SLO 5), and understanding and critiquing the reasoning of others (e.g. SLO 1).

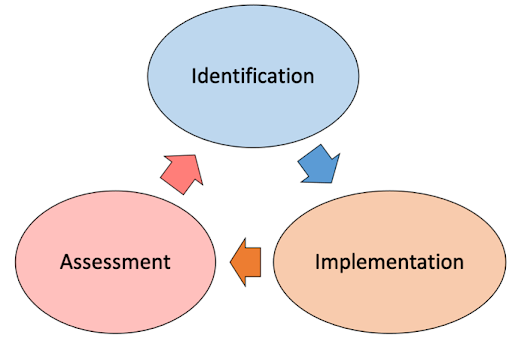
Studying our students’ and our own math practices has empowered us to support our students in developing these practices. As we describe in Chapter 47 of the GeT book, we study practices through a cycle of inquiry that involves: identifying evidence of math practices in student, creating & implementing tasks to engage them in those practice, and assessing their practices. This allows us to identify micro-practices: fine-grained skills that contribute to the development of a practice. Awareness of micro-practices enables us to provide explanations, orchestrate discussions, create tasks and assessments, and provide feedback that helps our students acquire math practices.

For example, by studying the practice of reasoning mathematically and constructing viable arguments (SLO 1) we identified a number of micro-practices that we can intentionally discuss, help students develop, and assess.  These include that mathematically proficient students:

1. Justify claims and solutions through a convincing explanation as to why it is correct, rather than simply telling how they solved it. 
2. Attend to the scope of a claim by providing examples and counterexamples, when they are sufficient, and broadly applicable arguments, when examples are insufficient. 
3. Ensure their arguments are complete by identifying and attending to the burden of proof.
4. Build their case by making valid and relevant claims. 
5. Provide detail by supporting all of their claims. 
6. Make valid deductions from appropriate axioms, definitions, and theorems to support their claims. 
7. Logically structure their arguments in valid ways, appropriately using direct proof, proof by contradiction, proof by contraposition, or proof by induction techniques. 

Knowing these, we help students develop them through tasks and assignments, discuss these outright, and use them in rubrics for grading and feedback.

The inquiry cycle has become a part of our ongoing work as teachers.  It gives us a way of exploring other math practices and support students in developing them.  The benefit of identifying micro-practices goes beyond our geometry classes.  It allows us to support student development across the curriculum and provide early mathematical experiences that contribute to our students’ development of productive mathematical practices. 

We encourage you to take a deeper look at how you implement mathematical practices in your own courses and begin your own study of your and your students’ math practices. For additional information on our cyclic approach and in-depth descriptions of aforementioned micro-practices, see our paper.

Suggested Citation

Belnap, J., and Parrott, A. (2025, June). Practices Empower our Students. GeT: The News!, (6)2. https://www.gripumich.org/v6-i2-sp2025/#practices-empower-our-students

Working Group Updates

Transformation Group Update

In the spring of 2025, the transformation group mainly focused on elaborating on a sequence of lessons that GeT instructors could insert into their course to teach the proof of the Side-Angle-Side (SAS) triangle congruence criterion from a transformation perspective. In the fall 2024 semester, Kevin McLeod incorporated a version of the SAS lesson sequence into his GeT course, and the group has been discussing how this iteration of the lesson went for the purposes of modifying the SAS sequence and identified ways to enhance the lesson plan materials to be more suitable for (novice) instructors. We have also been making progress on an observation protocol to use in lesson studies more generally. Group members have continued to write reflections after each meeting so that the group can later take a broader look at how the process of collaborating to create and modify the SAS lesson sequence and the observation protocol have gone. We anticipate continuing this work into the summer.

Because our regular facilitator, Julia StGoar (stgoarj@merrimack.edu), is currently on leave, you can reach out to our temporary facilitator, Steve Boyce (sboyce@pdx.edu) for more information.

Thursday Working Group Update

by Mara Markinson

The Thursday working group has met several times since the last newsletter. We explored the connections between the tasks developed by members of the ESLO Working Group during the 2023-2024 academic year and SLO 6. Our group is comprised of university mathematics professors, university mathematics teacher educators, and high school geometry teachers. At each meeting, we have focused on one task and discussed ideas for implementation, specifically related to technology. Our last meeting of the semester will be on May 15, 2025.

Wednesday Working Group Update

by Robert Bell

The Wednesday GeT Working group continued to discuss SLO 9: Non-Euclidean Geometry and, to a lesser extent, SLO 4: Axioms & Models. We discussed three of the GeT Book chapters (19, 26, and 27) in detail. These chapters focused on how to motivate the inclusion of non-Euclidean geometry in GeT courses; in particular, the articles included specific recommendations for physical models for classroom use, how to connect the more familiar spherical geometry with hyperbolic geometry, and further examples of non-Euclidean geometries such as taxicab geometry. The consensus was that there are many wonderful and detailed ideas in these articles and in many other resources that individuals in the group were familiar with. However, specific classroom modules or activities seem to not be easily accessible in a common location. So, we raised the question of whether our group might attempt to consolidate and organize these resources. Some in our group will not be able to continue in the fall. We would love to include additional community members in this group.

Member Highlight – Interview with Henry Escuadro

Closing Note

by Steve Boyce and Stephen Szydlik

Moving on:

As we close out this issue, we want to acknowledge the hard work of Anthony Davis and his contributions to this newsletter and the GRIP lab. Anthony will be leaving the GRIP lab this summer and is taking on a new role as an Education Specialist at the Detroit Zoological Society. Thanks so much Anthony!

Suggested Citation

Boyce, S. and Szydlik, S. (2025, June). Closing Note. GeT: The News!, (6)2. https://www.gripumich.org/v6-i2-sp2025/#closing-note

Did you get promoted? Win a grant? Have a baby? Buy a house? We would love to feature your news, whether professional or personal! Email us at GRIP@umich.edu.

To submit a paper to be highlighted in a future newsletter, please fill out this form.