
Table of Contents
- What are we trying to achieve when we teach Geometry for Teachers? by Patricio Herbst
- Essential Student Learning Objectives for GeT Courses by Nat Miller
- Proof: The Heart of the Geometry for Teachers Course by Sharon S. Vestal
- GeT to Know the Community: Priya Prasad
- Understanding Student Thinking on Transformation Congruence Proofs by Julia St. Goar
- Facilitating Mathematical Discourse Online by Claudine Margolis
- Upcoming Events

What are we trying to achieve when we teach Geometry for Teachers?
One of the goals of the GeT: A Pencil community is to improve the instructional capacity for high school geometry. Geometry courses for teachers can be instrumental in preparing teachers with that instructional capacity. It is pertinent to ask what evidence we can use to steer that mission. Unlike in the K-12 environment where curriculum development and implementation are used to ensure that instruction meets standards, the culture of college instruction is one founded on academic freedom; and instructors often take pride in the development of their own course materials. In this context where instructors may be doing different things, it is important to understand what could be meant by improvement and how we could know that we are improving instructional capacity.
The approach to improvement science espoused by Bryk et al. (2015) counters the usual paradigm of evaluation research, often focused on establishing the main effects of interventions, controlling for implementation fidelity. Bryk et al. (2015) consider it sensible that interventions will vary across sites as they attend to characteristics of their context. This aligns well with the situation in which each instructor of Geometry for Teachers designs and implements their course: Instructors know the students they usually have, their mathematical backgrounds, and other elements of their professional preparation. It would not be sensible to try to make all Geometry for Teachers courses alike.
However, based on analyses of healthcare operations, Bryk et al. (2015) propose that an alternative guide for improvement would try to reduce the variability in the outcomes of education interventions. In healthcare, outcomes might include various measures of patients’ health, such as the time-to-hospital-discharge by condition treated or the number of changes in treatment needed to achieve recovery. In terms of time to discharge, for example, we know that recovery depends not only on the efficiency of medical teams, but also on the condition and the patient’s comorbidities. Thus, to say that a healthcare provider is doing good quality work, it would not be sensible to expect the time to discharge to reduce to 0 or for all patients to take the same amount of time to recover. Yet, if predictions of the time to discharge gave a very large time interval, this large variability might suggest a possible focus for improvement. Instructional capacity for geometry teaching may also be seen as amenable for this kind of improvement. We know that there will always be things a teacher needs to know that they did not learn in our courses; we also know that there will always be things they had the opportunity to learn in our courses and yet they didn’t. How can we think about reducing the variability of outcomes of geometry courses for teachers in ways that allow us to gauge the improvement of our collective efforts to increase instructional capacity? What are some options for outcome variables whose variability we could aim to reduce?
One way of assessing the variability of outcomes could be to count credits among graduates, such as how many geometry courses a teacher had in their preparation. In the past, the number of mathematics courses a teacher had taken was believed to have an influence on teacher performance, but research has not been conclusive (Begle, 1979; Monk, 1994). In our experience surveying practicing high school geometry teachers, however, this number has shown very little variability to begin with, to the point that it does not even make sense to ask what its effects are on other teacher variables (e.g., the amount of mathematical knowledge for teaching).
A second way of assessing the reduction in variability of outcomes comes from the availability of scores in our MKT-G test (Herbst & Kosko, 2014; Ko & Herbst, 2020). The GRIP lab has surveyed a nationally distributed sample of practicing high school teachers using this instrument. We have also been using the MKT-G test at the beginning and at the end of the GeT course for students of instructors of the GeT: A Pencil community. As a result of implementing the test for several semesters and across several courses, we have gotten a sense of how much mathematical knowledge for teaching geometry students have when they start the course and how much they have when they end. On average they start at a score -1.10 and they end at -0.92 both below the standardized mean of practicing geometry teachers. Our current data suggests that the average students’ increase in MKT-G is about 0.18 standard deviations. As experience teaching geometry correlates with MKT-G scores, that increase of 0.18 SDs is equivalent to the growth that a teacher would have in 2.5 years of experience. While one way to think about improvement might urge us to try and increase that difference beyond 0.18 SD, we also know that such an increase is likely to be bounded as there is only so much learning that can happen in a semester.
The improvement approach would suggest that we look instead at whether the variability in outcomes reduces over time. For example, when students arrive at our GeT courses, what they know of geometry for teaching may vary widely depending on their prior experiences. At the end of the course, we would expect everybody to know more. But rather than only looking at this average growth, we could also look at the variability of individual growth. What is the variation in growth among the students in a class over the semesters? What is the variation in growth among the students of instructors in our community over the semesters? While increasing the amount of MKT-G score improvement is desirable, reducing the variability among those increases could help us argue that geometry for teachers courses are associated with predictable gains among individual prospective teachers.
Yet the MKT-G test is built on a conception of instructional capacity to do tasks of teaching high school geometry, in the context of instructional situations from the high school geometry course. As not all GeT courses are focused on that material, the MKT-G is not necessarily aligned with a shared conception of desirable outcomes by instructors of the course. It is reasonable to look for reductions in the variability in the growth of MKT-G scores but that by itself might not have the key to how to increase instructional capacity.
The recent effort by the Teaching GeT working group to develop a shared list of student learning outcomes (SLOs) helps move toward understanding what variability in outcomes we might want to aim to reduce. In this issue of the newsletter, Nat Miller introduces the effort and lists the student learning outcomes the Teaching GeT group developed over the 2019-2020 academic year. Another note, by Sharon Vestal, provides a commentary on the first of these SLOs. We are eager to publish commentaries on all of these SLOs, as well as written responses to published elaborations, or possibly complementary elaborations. The effort to identify SLOs rests on the notion that while we might be foolish to expect all GeT courses to be the same, mathematics departments in high schools, parents, and high school students are entitled to expect their geometry teachers to have some competencies. GeT instructors could choose many materials and pedagogical approaches to achieve those outcomes and as long as those outcomes are achieved, our community could stand behind any one of our graduates. But in order to be able to assess our improvement using these SLOs, it is really important to develop consensus on these SLOs. We hope the notes included in this newsletter and the following ones will help us move toward such consensus. It would then be sensible to survey students in regard to whether they have had, in their GeT courses, opportunities to learn aligned with each SLO. The notion of improvement in the sense of reduction in the variability of outcomes could be understood as having more and more students indicate that they have had opportunities to learn the same SLOs even if the ways in which those opportunities were provided varied.
As we develop consensus, it also seems important for us to try to integrate the developing SLOs into the framework of the MKT-G test, as we can use successive administrations of the test to calibrate and phase in new items that, over time, might also inform the assessment of growth among GeT students. MKT-G items usually pose a mathematics problem in the context of a task that a high school geometry teacher may need to do. Creating problems for their students, preparing materials for lessons, understanding what students do in response to problems, crafting explanations for key ideas, providing definitions, etc. are tasks a teacher has to do routinely. We hope that as the SLOs develop we might also hear suggestions as to how to create assessment items that might tap into the knowledge named in the SLOs. We anticipate that those items might help bring closer together the objectives GeT instructors have for their courses and the knowledge needed for teaching high school geometry. This effort may therefore help us track more accurately how we are improving instructional capacity for high school geometry.
References
Begle, E.G. (1979). Critical variables in mathematics education: Findings from a survey of the empirical literature. Washington, DC: Mathematical Association of America and National Council of Teachers of Mathematics.
Bryk, A. S., Gomez, L. M., Grunow, A., & LeMahieu, P. G. (2015). Learning to improve: How America’s schools can get better at getting better. Harvard Education Press.
Herbst, P., & Kosko, K. (2014). Mathematical knowledge for teaching and its specificity to high school geometry instruction. In J. Lo, K. R. Leatham, & L. R. Van Zoest (Eds.), Research Trends in Mathematics Teacher Education (pp. 23-45). New York, NY: Springer.
Ko, I., & Herbst, P. (2020). Subject matter knowledge of geometry needed in tasks of teaching: Relationship to prior geometry teaching experience. Forthcoming in Journal for Research in Mathematics Education, 51(5)
Monk, D. H. (1994). Subject area preparation of secondary mathematics and science teachers and student achievement. Economics of Education Review, 13(2), 125-145.
Suggested Citation
Herbst, P. (2020, October). What are we trying to achieve when we teach Geometry for Teachers? GeT: The News!, 2(1). https://www.gripumich.org/v2-i1-f2020/#what-are-we-trying-to-achieve-when-we-teach-geometry-for-teachers

Essential Student Learning Objectives for GeT Courses
by Nat Miller
Last year, the Teaching GeT (Geometry for Teachers) Group started to think about the question: what materials could we produce that would be most helpful for a new teacher of a GeT course? We quickly ran into an issue: unlike many other mathematical subjects, there isn’t a standard curriculum for a GeT course. Many different kinds of courses are taught, even among the members of the group. We therefore started to wonder how much agreement there was about the goals for such a course. Are all the different kinds of courses attempting to meet a common set of goals in different ways, or do the different courses have fundamentally different goals? This question has important implications for how we view what we are doing in a GeT course, how we provide professional development for new instructors of GeT courses, and how we determine if a GeT course is successful. As a group, we tried to come up with a list of shared goals for the GeT course in the form of SLOs (Student Learning Objectives). What we discovered was that, at least among the members of our group, there was a strong consensus about the major goals for a GeT course.
In order to arrive at our set of essential SLOs, we used a winnowing strategy. First, we asked members of the group to write down what each person thought were essential SLOs. I took everyone’s lists and combined them into a master list that contained all of everyone’s ideas. We looked at the master list as a group and winnowed it down to the ideas that everyone agreed were essential. I used these to create a draft list of SLOs. We put each SLO up on an online discussion board where different members of the group could make individual comments on each SLO. Finally, we went through all the comments as a group and refined the SLOs.
The SLOs that we developed dealt with 10 broad categories:
- Proofs Derive and explain geometric arguments and proofs in written and oral form.
- Proof Verification Decide whether or not geometric arguments given by others are correct.
- Secondary Geometry Understanding Understand the ideas underlying the typical secondary geometry curriculum well enough to explain them to their own students and use them to inform their own teaching.
- Axioms, Theorems, and Models Understand and explain the relationship between axioms, theorems, and geometric models in which they hold (such as the plane, the sphere, the hyperbolic plane, etc.).
- Definitions Understand the role of definitions in mathematical discourse.
- Technologies Effectively use technologies such as dynamic geometry software to explore geometry.
- Euclid’s Elements Demonstrate knowledge of Euclidean Geometry, including the history and basics of Euclid’s Elements, and its influence on math as a discipline.
- Straightedge and Compass Constructions Be able to perform basic Euclidean straightedge and compass constructions and be able to provide justification for why the procedure is correct.
- non-Euclidean Geometries Compare Euclidean geometry to other geometries such as hyperbolic or spherical geometry.
- NCTM Standards Apply the following NCTM Geometry Standards: (a) analyze characteristics and properties of two- and three-dimensional geometric shapes and develop mathematical arguments about geometric relationships; (b) apply transformations and use symmetry to analyze mathematical situations; and (c) use visualization, spatial reasoning, and geometric modeling to solve problems.
We included a statement that in addition to teaching these content standards, all Geometry courses for future teachers should give students many chances to experience and develop their abilities with the mathematical process skills of problem solving, reasoning and proof writing, oral and written communication of mathematical ideas, and productive collaboration within groups. They should also get a chance to engage with the progression of exploration followed by making conjectures, followed by trying to prove their conjectures.
Our hope is that we will be able to validate these goals with a wider cross-section of the community of people who teach GeT courses by verifying that most stakeholders also consider these to be the major goals of any GeT course. They can then serve as the basis for professional development, assessment, and evaluation efforts.
Suggested Citation
Miller, N. (2020, October). Essential Student Learning Objectives for GeT Courses. GeT: The News!, 2(1). https://www.gripumich.org/v2-i1-f2020/#essential-student-learning-objectives-for-get-courses

Proof: The Heart of the Geometry for Teachers Course
by Sharon S. Vestal
When I joined the Geometry for Teachers (GeT) group in the summer of 2018, one thing that was always clear to me was that the GeT course at various institutions is very different. During the 2019 – 2020 academic year the Teaching GeT group, led by Dr. Nat Miller, made a huge effort to create a common list of Student Learning Objectives (SLO) for the GeT course. The list needed to be concrete enough to help a faculty member teaching the course for the first time, yet flexible enough that it works for different institutions.
Since I feel that proof should be the focus of the GeT course, I will elaborate on the first Proof SLO, “Derive and explain geometric arguments and proofs in written and oral form.” In the study of mathematics, true understanding is attained when one can read and write a proof of a theorem, explain it to another person, and apply the theorem. Geometry is an area of mathematics for which this skill may be more easily attained because figures are frequently used to illustrate theorems. While one should never rely on a picture when completing a geometry proof, having an image is often helpful when writing a geometry proof.
Why is it important that future teachers have a solid background in proof? While not every state has adopted or uses the Common Core State Standards for Mathematics (CCSSM), many have written new mathematics standards that are very similar to these standards. In the CCSSM, the first mention of proof is in the 8th grade geometry standards. These standards focus on using rotations, translations, and reflections to demonstrate that two figures are congruent to one another, and students are expected to be able to explain a proof of the Pythagorean Theorem and its converse. In the CCSSM high school geometry standards, students are expected to “understand congruence in terms of rigid motion” and “prove geometric theorems,” (National Governors Association, 2010).
Can we expect secondary mathematics teachers to teach proof without undergoing it for themselves? Mathematics teachers need to experience geometry proofs from the student perspective so they can empathize when their own students struggle. They need to be able to understand different types of proofs, such as synthetic (from axioms), analytic (using coordinates), and proofs using transformations or symmetries. They should be able to communicate proofs in different ways (two-column, paragraph, or a sequence of transformations). It is also essential that they can choose the most accessible type of proof for the situation.

In an ideal world, students would enter the GeT course with a strong background in proof, but that is generally not the case. Some of the variation in their proof background depends on the level of the GeT course (200, 300, or 400), but much of it depends on their own high school geometry experience. Based on what the GeT students tell me, high school geometry likely has the most variability of all high school mathematics courses throughout our country. Some students never had to do proofs in their course, while others did a lot of proofs in various forms. This is one of the reasons that the GeT SLOs are so important—we cannot help improve the teaching of high school geometry without looking at our own teaching of geometry. Great teachers are reflective practitioners—what better way to produce strong mathematics teachers than to model this practice for our preservice teachers.
Writing a synthetic proof requires the ability to put together a logical argument in a systematic manner. This skill leads to growth in critical thinking and reasoning. Daily we encounter situations where critical thinking is needed. Geometry is the best course to use proof to help students build problem solving skills, which is why I believe that proof should be the heart of the GeT course.
References
National Governors Association Center for Best Practices, Council of Chief State School Officers. (2010). Common Core State Standards for Mathematics. Washington, DC.
Suggested Citation
Vestal, S. (2020, October). Proof: The Heart of the Geometry for Teachers Course. GeT: The News!, 2(1). https://www.gripumich.org/v2-i1-f2020/#proof-the-heart-of-the-geometry-for-teachers-course

Get to know the community
Four questions with Priya Prasad, Assistant Professor, Department of Mathematics, The University of Texas at San Antonio.
- What is special about your GeT course? We have been working on creating a course that focuses on using transformations ( i.e. rigid motions) as axioms. What I like about using this axiomatic approach is that it services preservice teachers well, as it is aligned with our state standards for K-12 geometry, and it is an approach that our math majors, who also take this course, should be introduced to.
- Who are your students? About forty percent are math majors who are taking applied mathematics and statistics track, forty percent are secondary preservice teachers, and twenty percent are preservice middle school teachers.
- What are you most interested in learning/achieving through participating with the GeT: A Pencil community? I am interested to learn abouI am interested in learning about what other instructors do and to situate myself in the community of GeT instructors. I have learned that because we all have different contexts and student populations specific to our institutions, it is not going to be possible to create a prototypical GeT course. However, it is interesting to learn where there is convergence of ideas and convergence of approaches, especially because there is this distinction of contexts.

- What is your favorite book you have read in the last few years? I am interested in learning about what other instructors do and to situate myself in the community of GeT instructors. I have learned that because we all have different contexts and student populations specific to our institutions, it is not going to be possible to create a prototypical GeT course. However, it is interesting to learn where there is convergence of ideas and convergence of approaches, especially because there is this distinction of contexts.
Did you get promoted? Win a grant? Have a baby? Buy a house? We would love to feature your news, whether professional or personal! Email us at GRIP@umich.edu.

Understanding Student Thinking on Transformation Congruence Proofs
by Julia St. Goar
In recent years, a transformation perspective has come to the fore in K-12 standards (National Governors Association Center for Best Practices, Council of Chief State School Officers, 2010; NCTM, 2018) leading many college instructors to transition their geometry for teachers courses to include transformation geometry. Unfortunately, at any level, there has been “limited research explicitly on the topics of congruency and similarity, and little on transformation geometry” (Jones & Tzekaki, 2016, p. 139).
In order to support instructors working to incorporate a transformation context into their course, Dr. Yvonne Lai (University of Nebraska-Lincoln) and I have worked to more carefully understand student thinking on transformation congruence proofs (St. Goar & Lai, 2019, 2020). Much of our work focuses on how students understand and use the definition of congruence, which states that two figures are considered congruent if, and only if, there exists a sequence of transformations (translations, reflections, and rotations) that maps one object to the other.
In the course of our research so far, we have analyzed student work on transformation congruence proofs from homework and exams in two geometry for teachers courses; one taught at UNL and the other at Merrimack College. We have analyzed student work on many different problems, and student work on the Boomerang Problem and the Line-Point Problem (Figure 1) proved to be particularly enlightening for this research.
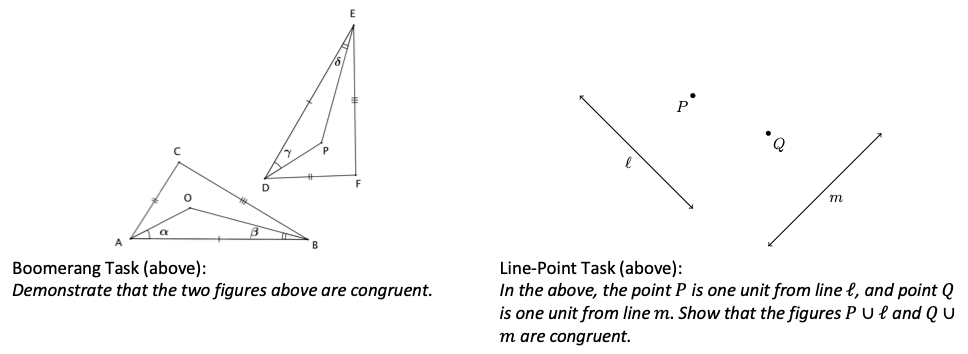
Our analysis uncovered possible key developmental understandings (Simon, 2006) as students work to employ the definition of congruence in proof. As a brief summary, a key developmental understanding (KDU) affords the learner a different way of thinking about mathematical relationships, and learners acquire KDUs through reflection and multiple experiences – not by direct explanation. As a result, special care may be needed to reinforce KDUs repeatedly throughout a term and in many different contexts. In a transformation congruence proof context, we identified the following potential KDU’s:
- Understanding that applying the definition of congruence to prove congruence of two figures means establishing a sequence of rigid motions mapping one entire figure to the other entire figure.
- Understanding that using a sequence of transformations to prove that two figures are congruent means justifying deductively that the image of one figure under the sequence of transformations is exactly the other figure.
To clarify, a student who doesn’t show evidence of the first potential KDU above may still know that rigid motions are involved in a transformation congruence proof. However, they may not realize that a figure must remain intact and unaltered throughout the transformation process. For example, when looking at student work on the Boomerang Problem, we found that some students would apply different rigid motions to each triangle. Some of these students might then conclude that because ∆ABC≅∆DEF and ∆ABO≅∆DEP, that the union of these triangles is also congruent.
Understanding the second potential KDU involves realizing that successfully identifying a candidate sequence of transformations between two figures isn’t sufficient to demonstrate congruence between the two figures. For example, on the line-point problem, some students correctly constructed sequences of rigid motions from one entire figure (i.e. the union of the line and the point) to the other entire figure, yet the students stopped short of making an argument explaining why the rigid motions caused the two figures to be superimposed. In some of these cases, we suspect students are viewing these figures as already superimposed and thus may not grasp why this justification is necessary.
This research has helped us to illuminate the perspectives of the students in our geometry for teachers courses to provide better feedback to students during group work and, when correcting their work, to become aware of concepts that need to be repeatedly reinforced in lesson plans and assignments. We hope readers will be able to do the same and to find new ways to apply these perspectives to their courses.
Acknowledgements
This work is partially supported by NSF DUE- 1937512. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the NSF.
References
Jones, K., & Tzekaki, M. (2016). Research on the teaching and learning of geometry. In A. Gutiérrez, G. Leder & P. Boero (Eds.), The Second Handbook of Research on the Psychology of Mathematics Education: The Journey Continues (pp. 109-149). Rotterdam: Sense.
National Council of Teachers of Mathematics. (2018). Catalyzing change in high school mathematics: Initiating critical conversations. Reston, VA: Author.
National Governors Association Center for Best Practices, Council of Chief State School Officers. (2010). Common Core State Standards for mathematics. Washington, DC: Author.
Simon, M. A. (2006). Key developmental understandings in mathematics: A direction for investigating and establishing learning goals. Mathematical Thinking and Learning, 8(4), 359-371.
St. Goar, J., & Lai, Y. (2019). Prospective High School Teachers Understanding and Application of the Connection Between Congruence and Transformation in Congruence Proofs. Weinberg, A., Moore-Russo, D., Soto, H., & Wawro, M. (Eds.), Proceedings of the 22nd Annual Conference on Research on Undergraduate Mathematics Education, (pp. 247-254). Oklahoma City, OK.
St. Goar, J. & Lai, Y. (2020). Defining Key Developmental Understandings in Congruence Proofs from a Transformation Approach. Karunakaran, S., Reed, Z., & Higgins, A. (Eds.), Proceedings of the 23rd Annual Conference on Research in Undergraduate Mathematics Education, (pp. 880-885). Boston, MA.
Suggested Citation
St.Goar, J. (2020, October). Understanding Student Thinking on Transformation Congruence Proofs. GeT: The News!, 2(1). https://www.gripumich.org/v2-i1-f2020/#understanding-student-thinking-on-transformation-congruence-proofs

Facilitating Mathematical Discourse Online
by Claudine Margolis
“Social interaction provides us with the opportunity to use others as resources, to share our ideas with others, and to participate in the joint construction of knowledge.”
(Smith & Stein, 2011, p. 1)
The rapid transition to online instruction in the spring forced many instructors to develop remote learning strategies that sacrificed high-quality instructional practices out of necessity or institutional policy. Without proper support or training, many instructors are grappling with the same challenges this fall; in particular, creating opportunities for students to engage in collaborative problem-based learning requires that instructors have a combination of technological fluency and knowledge of effective online teaching moves. Although the resources below are not comprehensive, they provide a starting place for considering the challenges and opportunities associated with online mathematics instruction.
Teaching mathematics online requires us to rethink the way classrooms and interactions are organized. I see three main considerations: (1) the organization of materials (e.g., tasks, manipulatives, agenda/goals), (2) the organization of people (e.g., flexible groupings, individual work, whole-class), and (3) the organization of ideas (e.g., shared written mathematical thinking, formative assessments).
Organization of Materials
An essential component of problem-based learning is the mathematical task that students engage with, so the success of a lesson can hinge on how well an instructor launches the task. Doing this well requires that students know what they are supposed to be doing, how they are supposed to be doing it, and who they should be working with. Online learning environments make it much more likely that students will miss some part of the launch discussion or forget part of the directions. In a classroom, they can just lean over to a groupmate and ask for help, but now they are physically and technologically isolated from their peers.
To address this challenge, use a consistent format for sharing your agenda, lesson objective, manipulatives, and expectations for class. See slides 3-11 of the additional resources.

Organization of People
To facilitate engaging and productive collaborative learning, we need to be able to group students in multiple ways. You can assign students to breakout rooms for small-group collaborative work in Zoom, BigBlueButton, or BlueJeans. If you want students to be able to choose their own groups, try Congregate or use multiple video calls and allow students to choose which room they go into. See slides 12-13 of the additional resources.
Organization of Ideas
To close a collaborative problem-based mathematics lesson, I try to use a variety of questioning strategies to make visible the relevant mathematics in a way that moves all students toward accomplishing the learning goals. When transitioning to the online environment, it’s important to have specific strategies for facilitating those discussions or you’re likely to get blank stares and silence as responses to what would normally be an engaging question. It’s important to recognize that online discussions are not just regular whole-class discussions through a new medium. Video conferencing software allows students to engage in fundamentally different ways that can be leveraged to increase participation by all students. The list below has strategies that enable all students to participate. See slides 14-17 of the additional resources.
- Virtual whiparound (slide 15).
- Use a Desmos Classroom Activity and utilize the Snapshots feature to put multiple pieces of student work in conversation with each other.
- Pose a question and ask students to write their response in the chat, but wait to press enter until you give the cue. When you’re ready, prompt them to submit their responses and then have everyone take a minute to read through them.
- Pose a question and then do a virtual Turn and Talk. Assign partners and have them initiate a private chat with each other to discuss the question. Have each pair use the “raise hand” reaction when they are done discussing. Alternatively, randomly assign pairs to breakout rooms for a few minutes.
- Ask students to respond to questions with other online resources, like Google Forms, Poll Everywhere, or Mentimeter (I like the data displays on this one).
- Have one student from each group annotate the screen to show their work for a problem, report out on a jigsaw, or write down a lingering question.
- Have all students respond to a question with nonverbal feedback on Zoom.
Suggested Citation
Margolis, C. (2020, October). Facilitating Mathematical Discourse Online. GeT: The News!, 2(1). https://www.gripumich.org/v2-i1-f2020/#facilitating-mathematical-discourse-online

Upcoming Events
What geometry should secondary teachers learn, and what geometry should they teach?
Friday, October 30 3:00 pm ET via Zoom
Animated Contrasting Cases in Geometry (AC2inG): The Design of New Geometry Curricular Modules
Friday, November 6 2:00 am ET via Zoom
Diagrams in Euclidean Geometry: Logical, Philosophical, and Pedagogical Considerations
Friday, November 13 3:00 pm ET via Zoom
GeT Support
Sponsored by NSF DUE-1725837. All opinions are those of the authors and do not necessarily represent the views of the National Science Foundation or the University of Michigan.
Patricio Herbst, PI
Amanda Milewski, Co-PI
Inese Berzina Pitcher, Project Manager, Get: The News Editor
Get Support is housed in the GRIP Lab at the University of Michigan
