
Table of Contents
- 2021: Looking Back, Looking Forward by Amanda Milewski
- Get Activity: People and Clubs: An Axiomatic System by Stephan Szydlik
- New Transformation Working Group Summary before the start of Spring 2021 by Julia St. Goar
- Narratives for the Essential SLOs for GeT Courses by Nathaniel Miller
- GeT Course Student Learning Outcome #4 by Teaching GeT Working Group Members
- GeT to Know the Community: Tuyin An
- Upcoming Events

2021: Looking Back, Looking Forward
by Amanda Milewski
With 2020 in the rearview mirror, we take a moment to pause and reflect on some of what’s happened since the last newsletter. The rising incidence of COVID-19 infections brought with it a massive upheaval for American higher education institutions—forcing students, in many cases, to vacate dorms, and instructors to rapidly transition from hybrid to exclusively online forms of instruction. While this upending of “business as usual” has certainly come with its share of unique and difficult challenges, we have heard from you that it has also provided some surprising and uncommon opportunities. This fall, the ubiquitous use of online and hybrid instruction provided us the possibility and privilege of peering into some of your classrooms. We’d like to share some of what we learned.
We would be remiss if we didn’t acknowledge the challenges that this time period has created for undergraduate students. For one, the disruptions to more routine university life has brought unique logistical challenges for undergraduates. In the moments between problems in one small group, we overheard one student sharing about the struggles she was having with the university’s decision to leave some courses in-person and others remote—putting her in a situation in which her parents insisted she save money and move home only to face several two-hour commutes over snowy roads for her one in-person class. We also observed ways that the sweeping changes to university life has left students feeling uncertain about their futures. In another small group exchange, two students discussed their fears regarding their ability to make progress in their teacher preparation programs with local districts and mentor teachers feeling too overwhelmed to make room for university students’ field placements. Also, we observed ways that these shifts have forced many students to blend their various roles (i.e., in addition to being students, they have familial obligations to their siblings, parents, and sometimes spouses or children) making it more challenging, at times, to focus on their role as students. For example, in the midst of a virtual whole class debate about whether or not Euclid’s third axiom holds in hyperbolic space, we observed one student splitting her attention between the small wiggly child in her lap and taking her turn in the debate—sometimes struggling (understandably) to keep her train of thought.
Yet, in the face of these challenges, we were consistently impressed with the innovative ways that both instructors and students worked collectively to maintain some semblance of normalcy in instruction. We observed instructors and students making use of physical manipulatives to maintain students’ engagement with instructional activities. One instructor told us how, in order to avoid the risk of spreading the virus, she organized and distributed physical manipulatives at the start of the semester to enable students to gain familiarity with the kinds of resources they will eventually need to use in their work as high school teachers. Another instructor supported students over video conferencing to construct their own 450-degree cone out of construction paper and then used these cones in a series of investigations exploring the viability of Euclid’s postulates on the 450-degree cone.
Beyond the use of physical manipulatives, we also saw familiar technologies being leveraged in creative ways to support teaching and learning in the GeT courses we observed. Technologies as simple as document cameras, video cameras, and even social media were leveraged by instructors and students alike to not only cope with but also thrive in the current situation. On numerous occasions, we even watched as students helped one another and the instructor out by using social media platforms, such as Snapchat and Instagram, to share course files with other students. In some cases, instructors have shared how they have identified new practices during this time that they intend to keep—even after the pandemic is behind us. For example, one instructor shared her plans to continue taking advantage of newly-installed classroom cameras to record students’ mathematical presentations, enabling students to reflect on and improve their communication skills. Another instructor shared plans to maintain virtual office hours for students—noticing a substantial increase in students’ participation.
We also saw instructors and students making use of math-specific technologies to overcome their diverse geographic locations. For example, in a hybrid GeT course, students were managing (in spite of their geographic distance) to collectively communicate and reason about proofs using dynamic geometry software. Crucially, students had learned to harness the functionalities of Geometer’s Sketchpad to remotely walk through the steps of their proofs—simultaneously highlighting statements in their proof and corresponding elements of the given diagram (see Figure 1).
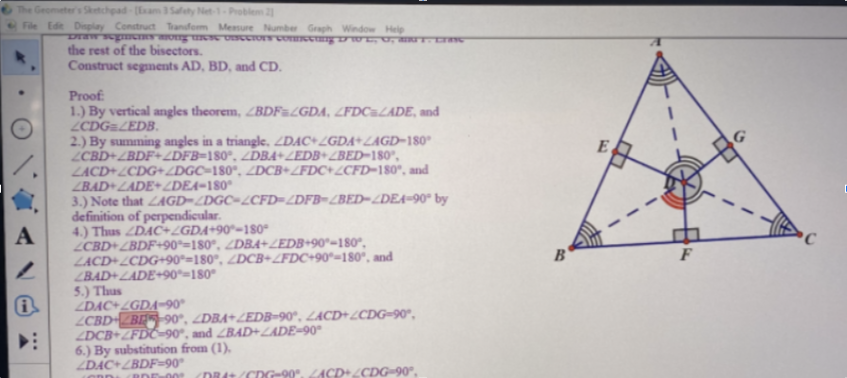
The students’ used this functionality to participate in a core mathematical practice of listening and critiquing one another’s proofs. Also, this use of Sketchpad enabled a kind of dynamic form of mathematical communication in which a single gesture towards a proof statement is intrinsically linked with the corresponding aspect of the geometric diagram that we think has potential beyond this current season of disruption to normal instruction. In all cases, we saw instructors and students finding ways to use the tools they had available to communicate about new and powerful ideas for students’ mathematical development.
Overall, what we saw while “sitting in the back of your classrooms” left us curious about the future. We found ourselves wondering what kinds of pedagogical practices students in these courses were having opportunities to “apprentice” into. We think it’s possible that this cohort of students is more ready than any previous cohort for engaging in online teaching, which may take the field a long way towards the goal of increasing the capacity for teaching high school geometry. We also wondered whether pre-service teachers would translate the kinds of practices they are learning, such as the use of Sketchpad to communicate dynamically about their proofs, into their future professional work. And while we, like you, long for things to return to some semblance of normal, we also found ourselves hopeful regarding the kind of resolve and commitment we saw in both GeT students and instructors. We think it’s possible that undergraduate mathematics instructors and their students will come out of this difficult season stronger and more ready to engage in mathematics education for the 21st century.
Suggested Citation
Milewski, A. (2021, February). 2021: Looking Back, Looking Forward. GeT: The News!, (2)2. https://www.gripumich.org/v2-i2-w2021/#2021:-looking-back-looking-forward

People and Clubs: An Axiomatic System
by Stephen Szydlik
“One must be able to say at all times – instead of points, straight lines, and planes – tables, chairs, and beer mugs. “
David Hilbert [4]
Axioms serve as fundamental bricks in the foundations of mathematics. Given a small collection of statements assumed to be true, a universe of subsequent truths may spring forth, grounded in those assumptions and constructed using mathematical logic. Change the axioms even slightly and you change that mathematical world. In geometry, the collective reconsideration of Euclid’s Fifth Postulate and the alternatives offered up in its place led to the “strange new universe” of hyperbolic geometry created by János Bolyai and others. [2]
Students at the onset of a GeT course typically have at least a passing understanding of proof, and many have taken a university course focusing on sets, logic, and proof structure. However, students generally have little experience with axioms beyond the definition of the term. Nevertheless, developing a sense of axioms and axiomatic systems is essential to understanding the nature of mathematics. A GeT course provides a natural place in the undergraduate curriculum to address this important concept.
One problem that I have used in my GeT course for many years to introduce the idea of axiom systems was developed by a group of mathematicians at the University of Wisconsin in the early 1990s:

The axioms here are essentially those for a finite affine geometry with “people” and “clubs” playing the respective roles of points and lines. Notably, Axiom H4 is a disguised version of Playfair’s postulate, logically equivalent in Neutral Geometry to Euclid V. Disguising the axioms serves a pedagogical purpose. Students’ familiarity with Euclidean notions of points and lines comes with some baggage;they often hold tacit assumptions about the relationship between points and lines (e.g., lines are “straight,” and if two lines look like they intersect, then they do, at a point). These assumptions tend to impede their ability to grapple with the consequences of the axioms for geometry on a purely logical basis. Framing the problem in terms of “people” and “clubs” counteracts that tendency and encourages students to prove statements by relying solely on the axioms.
I should note that while the GeT course that I teach centers around axioms and the Euclidean archetype [3], this activity neither requires nor expects students to possess a deep understanding of axioms. In fact, I typically use it as a “first day” problem to introduce them to axioms and the desirable properties of axiom systems. I have also used the problem successfully in a lower-level geometry course for non-majors. On the other hand, the problem allows for further deep investigation; the clubs in the town of Hilbert have a rich structure!
“People and Clubs” offers students opportunities to model, to construct viable arguments, and to reason abstractly, processes highly valued by our community and advocated by educators. [1] Students model the problem in several different ways. Some use letters (or numbers) to represent the n people in Hilbert, and sets of those letters as clubs (e.g. “BDE” as a three person club). Others provide visual representations with people as dots, containing ovals showing club membership.
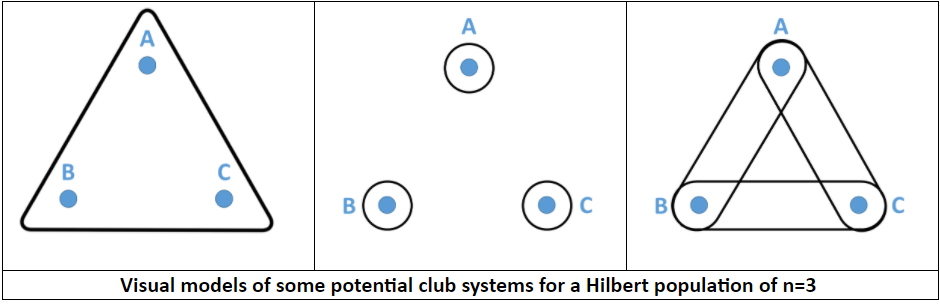
Regardless of representation, however, students are generally able to dispose of the n=2 population rapidly since determining its viability does not require the use of Axiom H4. Students tend to find that fourth axiom thorny, in part because the statement involves both the existence and uniqueness of a particular club. When they understand this language, they are better able to see the logical difficulties with a 3-person town. In our class discussion, I challenge them with several different examples of impossible 3-person systems (see the picture below). For example, the system consisting of strictly two person clubs illustrated in the third example violates the “existence” clause of Axiom H4: Given club AB and person C, there is no club that contains C that has no members in common with AB. Challenging students with examples such as this encourages them to make explicit their use of the axioms—a skill that becomes useful when investigating larger Hilbert populations and that is critical when considering the extreme cases of n=0 and n=1.
Perhaps the most interesting situation that we consider in class is a 5-person Hilbert. A careful analysis of the smaller population situations pays off here because a direct proof of the impossibility of the n=5 population requires several cases. In my classes, students are often initially uncertain about whether a town of this size is possible. Many believe that a system consisting entirely of 2-person clubs is possible, as it is in an n=4 person town. Others may think that at least one of the other 5-person systems is valid. The identification and disposal of the cases offers opportunities for an intellectually satisfying discussion. For example, a system of 2-person clubs violates the “uniqueness” clause of Axiom H4: Given club AB and person C, there are two clubs (CD and CE) that contain C and have no members in common with AB. The table below illustrates some (but not all!) of the possible 5-person club systems and where they go wrong:
| Potential Club System for n=5 | Axiom Violation |
| AB, AC, AD, AE, BC, BD, BE, CD, CE, DE | (H4) “Uniqueness” |
| ABC, AD, AE, BD, BE, CD, CE, DE | (H4) “Uniqueness” |
| ABCD, AE, CE, BE, DE | (H4) “Existence” |
| ABCDE | (H3) |
Discussion of the “People and Clubs” problem typically takes about one class period, though I often ask my students to spend an evening considering the 5-person Hilbert situation. The activity works well as a standalone problem, and GeT instructors who do not teach an axiom focused course may wish to stop here. On the other hand, a deeper analysis of the problem in a GeT course can pay dividends throughout the semester in several ways. First, it can help students identify important general properties of axiomatic systems. For example, adding the axiom “(H5): There are five people in Hilbert,” quickly leads us to the notion of consistency. On the other hand, “(H5): There are not five people in Hilbert,” creates a redundant axiom system since we can prove that statement.
Second, the problem offers meaningful examples of models of an axiomatic system. This is particularly helpful when discussing independence of axioms: an axiom “(H5) There are four people in Hilbert” is independent since we can find models of (H1)-(H4) where the (H5) holds (the n=4 Hilbert case), and other models (e.g., n=0, 1) where (H5) fails. Finally, “People and Clubs” supports further mathematical exploration and conversation. The trivial case n=0, for example, provides an occasion to highlight the importance of precise language and interpretation of quantifiers. For deeper exploration, I will often have students try to prove (or disprove) statements that rely heavily on Axiom (H4). For example, if clubs X and Y have no members in common and Y and a third club Z have no members in common, then can we conclude that X and Z have no members in common? A series of questions such as this, perhaps posed as true/false statements, affords opportunities for students to practice making arguments within the system and in refining general proof skills. Other potential questions are included below.

References
- National Governors Association Center for Best Practices & Council of Chief State School Officers. (2010). Common Core State Standards for Mathematics. Washington, DC: Authors.
- Greenberg, Marvin Jay. Euclidean and Non-Euclidean Geometries: Development and History. W.H. Freeman and Company, 2008.
- Grover, B.W., Connor, J. Characteristics of the College Geometry Course for Preservice Secondary Teachers. Journal of Mathematics Teacher Education 3, 47–67 (2000). https://doi.org/10.1023/A:1009921628065.
- Reid, C. (1970). Tables, Chairs, and Beer Mugs. In Hilbert (pp. 57-64). Springer, Berlin, Heidelberg.
Suggested Citation
Szydlik, S. (2021, February). People and Clubs: An Axiomatic System. GeT: The News!, (2)2. https://www.gripumich.org/v2-i2-w2021/#people-and-clubs:-an-axiomatic-system

New Transformation Working Group Summary before the Start of Spring 2021
by Julia St. Goar
The transformation group has two ongoing complementary goals of 1) collecting and creating activities that help support foundational concepts in a transformation geometry context and 2) formulating an axiomatic system such that (a) its statements are accessible to both college geometry students and high school students and (b) the axioms lead to an efficient system of lemmas and propositions that can be used to deduce major congruence and similarity results. At its start over a year ago, goal (2) was the primary objective, but since then the group has been shifting its focus more towards goal (1).
To advance goal (1) over the summer of 2020, members of the group presented activities from transformation geometry they had already created or seen. In the fall of 2020, the group read Transformational proof in high school geometry: A guide for teachers and curriculum developers by Douglas and Picciotto and decided for the spring of 2021 to try to use the structure of axioms, definitions, and basic properties in the document as a foundation for collecting and creating a coherent set of activities. It is our intent that using this document will provide a way to more clearly organize and sequence activities, including those that the group has already collected. This process will likely start with working on activities that support future teachers’ understanding of the early postulates and definitions in the document and move later to more complex proofs and properties. However, the group will also continue its discussion of ways to expand on the early structure of the document, including the addition of more axioms, definitions, and notation to support certain teaching goals. A long-term goal of this process would be to create a shareable document to aid instructors who currently use or want to use transformations in their GeT courses.
The Transformations group meets every other Wednesday at 11:00 AM ET. The group welcomes new members.
References
1. Douglas, L. & Picciotto, H. (March, 2018). Transformational proof in high school geometry: A guide for teachers and curriculum developers. Retrieved from https://www.mathedpage.org/transformations/proof/transformational-proof.pdf
Suggested Citation
St. Goar, J. (2021, February). New Transformation Working Group Summary before the Start of Spring 2021. GeT: The News!, (2)2. https://www.gripumich.org/v2-i2-w2021/#new-transformation-working-group-summary-before-the-start-of-spring-2021

Narratives for the Essential SLOs for GeT Courses
by Nathaniel Miller
During the 2019-2020 academic year, the Teaching GeT working group developed a set of Student Learning Objectives (SLOs) for the GeT courses. This year, the working group is still focused on the SLOs. We are working on writing narratives elaborating on each SLO. An example draft narrative for one of the SLOs, SLO 4 on Axioms, Theorems, and Models, is included elsewhere in this newsletter. Over the rest of the academic year, we intend to complete similar narratives for each of the SLOs.
In addition, members of the working group submitted a proposal for a chapter on the SLOs in an upcoming book in the AMTE Professional Book Series to be called Reflection on Past, Present and Future: Paving the Way for the Future of Mathematics Teacher Education. Contributing to the proposal were working group members Tuyin An, Steven Boyce, Steve Cohen, Henry Escuadro, Erin Krupa, Nathaniel Miller, Laura Pyzdrowski, Ruthmae Sears, Stephen Szydlik, and Sharon Vestal, along with GeT: a Pencil leaders Pat Herbst and Amanda Milewski. We hope to hear by March whether or not this proposal has been accepted. If it is accepted, we plan to incorporate the narratives that we are working on into this chapter.
The SLOs deal with 10 broad categories:
- Proofs: Derive and explain geometric arguments and proofs in written and oral form.
- Proof Verification: Decide whether or not geometric arguments given by others are correct.
- Secondary Geometry Understanding: Understand the ideas underlying the typical secondary geometry curriculum well enough to explain them to their own students and use them to inform their own teaching.
- Axioms, Theorems, and Models: Understand and explain the relationship between axioms, theorems, and geometric models in which they hold (such as the plane, the sphere, the hyperbolic plane, etc.).
- Definitions: Understand the role of definitions in mathematical discourse.
- Technologies: Effectively use technologies such as dynamic geometry software to explore geometry.
- Euclid’s Elements: Demonstrate knowledge of Euclidean Geometry, including the history and basics of Euclid’s Elements, and its influence on math as a discipline.
- Straightedge and Compass Constructions: Be able to perform basic Euclidean straightedge and compass constructions and to provide justification for why the procedure is correct.
- Non-Euclidean Geometries: Compare Euclidean geometry to other geometries such as hyperbolic or spherical geometry.
- NCTM Standards: Apply the following NCTM Geometry Standards: (a) analyze characteristics and properties of two- and three-dimensional geometric shapes and develop mathematical arguments about geometric relationships; (b) apply transformations and use symmetry to analyze mathematical situations; and (c) use visualization, spatial reasoning, and geometric modeling to solve problems.
In addition to the SLOs, we included a statement that in addition to teaching these content standards, all geometry courses for future teachers should give students many chances to experience and develop their abilities with the mathematical process skills of problem solving, reasoning and proof writing, oral and written communication of mathematical ideas, and productive collaboration within groups. They should also get a chance to engage with the progression of exploration followed by making conjectures, followed by trying to prove their conjectures.
The working group will be meeting every other week throughout the spring semester, alternating between Wednesdays at 2 pm Eastern and Fridays at 11 am Eastern. We would welcome any members of the larger community who are interested in joining us for this important work.
Suggested Citation
Miller, N. (2021, February). Narratives for the Essential SLOs for GeT Courses. GeT: The News!, (2)2. https://www.gripumich.org/v2-i2-w2021/#narratives-for-the-essential-slos-for-get-courses

GeT Course Student Learning Outcome #4
by Teaching GeT Working Group Members
Understand and explain the relationship between axioms, theorems, and geometric models in which they hold (such as the plane, the sphere, the hyperbolic plane, etc.); understand how knowledge about different models can help us understand which theorems can be proven from a given set of axioms.
a) Recognize and be able to communicate the distinction between an axiom and a theorem and describe how mathematical systems arise from axioms.
b) Construct logical arguments within the constraints of an axiom system.
c) Understand the roles of models in determining the independence of axioms and the validity of proofs.
Geometry courses are one of the few places we talk explicitly about axiom systems with our students. Most teachers of college geometry classes will be familiar with the idea that it is possible for mathematical subjects to be reduced to a set of axioms and then a set of theorems proven (exclusively) from those axioms. However, even though this can be done in principle, it is something that working mathematicians rarely do outside of geometry and logic classes, so not everyone teaching a geometry class will have a lot of experience working with axiom systems.
In building an axiom system, we begin with undefined terms as well as with statements, called axioms, that are accepted to be true without proof. In geometry, the undefined terms include “points” and “lines”. The axioms establish assumptions about undefined terms and the relationships between them. A world in which we can give meanings to all of those terms is called an interpretation of the terms. For example, if we are talking about “points” and “lines,” we could interpret them as points and lines in the Euclidean plane, but we could also interpret them as points and great circles on the sphere. An interpretation is called a model of the axioms if all of the axioms are true in the interpretation. For example, if we have an axiom that says that two points lie on a unique line, the Euclidean plane would be a model of this axiom. The sphere would not because antipodal points like the north and south pole on the sphere can be connected by many different great circles
Axioms within a system are independent if no axiom in the system is a logical consequence of the others. This means that for any axiom, we should be able to find an interpretation in which that axiom fails, but all of the others are true. Models and independence are intimately tied into the history of geometry. Perhaps the biggest question about Euclid’s axiom system was whether his fifth postulate could be proven from his first four axioms. Although an apparently consistent hyperbolic geometry was developed in the early 1800s, it was not until Beltrami presented a model for that system later in the century that the independence of the parallel postulate was established.
A theorem is a statement that has been proven from the axioms without regard to interpretation. In a college geometry class, proof can be thought of as a convincing deductive argument relying on explicit reference to axioms or previously proven theorems. Since a model of an axiom system is an interpretation of the undefined terms that satisfies the axioms, every theorem translates to a true statement in a model. Therefore, if a mathematical statement turns out to be false in a model, then the statement cannot be a theorem, i.e. it cannot be proved from the axioms. Moreover, just as models can be used to show that a statement cannot be proven, they can show that a statement cannot be disproven. That is, demonstrating a model where a statement holds shows that the negation of the statement is not a theorem. Models, therefore, serve as a sort of laboratory for geometric conjectures and can be a powerful tool for exploring the properties of an axiom system.
Students need to understand what the axioms mean, and then they can try to convince someone that a theorem is true whenever the axioms are true. As in other parts of the geometry curriculum, we see a trade-off between trying to be as rigorous as possible and trying to be developmentally appropriate. Because this is the main place for considering axiom systems in the college math curriculum, understanding of the elements of an axiom system (axioms, models, theorems, interpretations, undefined terms) should be an explicit learning goal. Considering interpretations where axioms do not hold is a good starting point. It encourages students to grapple with what the axioms actually mean, their distinction from other axiomatic elements, and their role as a foundation of mathematical systems. This is, therefore, a natural place to bring non-Euclidean geometries into the picture.
When choosing how to introduce an axiom system, instructors must balance the need to establish expectations for axiomatic proof with the need to understand significant, non-obvious geometric results in a reasonable amount of time. In many classes, students start out with a very simple axiom system of basic facts true in almost any geometry and then proceed to prove theorems from them. A common approach is to introduce an axiom system consisting of Euclid’s axioms without the parallel postulate, which is used to develop a “neutral geometry”. This has the advantage of making the axioms simple enough to focus on the logic of building deductive inferences using them. One strategy for motivating students to reason axiomatically about neutral geometry is to introduce problems with rules in which undefined terms “points” and “lines” have been replaced either with nonsense terms (“Every Fo has two Fes.”) or with some other context (“Every club has at least two members.”). This encourages students to reason from the stated rules rather than using their geometric intuition.
When considering an axiomatic development of geometry, it is important to consider the developmental readiness of one’s students for reasoning abstractly. Although GeT students should have learned some elements of the Euclidean geometric system in their K-12 geometry curriculum, it can be helpful if the instructor starts with lower Van Hiele level tasks to scaffold students’ development of geometric reasoning and proof, especially with the consideration that GeT students are often from different STEM majors with varied prior knowledge. Varying expectations of rigour and abstraction can also provide opportunities for assessing students’ development of deductive reasoning (e.g., their application of logic) that is not purely axiomatic. Highlighting differences in expectations for justifications can help to solidify students’ understandings of the elements of axiom systems and proofs.
Suggested Citation
An T., Boyce, S., Cohen, S., Escuadro H., Krupa E., Miller N., Pyzdrowski L., Szydlik S., & Vestal S. (2021, February). GeT Course Student Learning Outcome #4. GeT: The News!, 2(2). https://www.gripumich.org/v2-i2-w2021/#get-course-student-learning-outcome-4

Get to know the community
Four questions with Tuyin An, Assistant Professor of Mathematics, Georgia Southern University
- What is special about your GeT course? In 2-3 sentences, describe your GeT course. My GeT course is an upper-level elective course for STEM majors that mainly covers the study of the axiomatic system in Euclidean geometry. This course is also a required course for Secondary Education B.S.Ed. majors to provide preservice teachers with an advanced understanding of geometry that will give them deeper insights when teaching. The course is mainly taught in a traditional lecture format with active learning activities.
- Who are your students? My GeT course usually has a mixed body of secondary preservice teachers and other STEM majors. I also teach a few other math content courses for K-8 preservice teachers.
- What are you most interested in learning/achieving through participating with the GeT: A Pencil community? I am interested in meeting other math teacher educators and mathematicians who also teach a GeT course, sharing our teaching experience, and discussing issues and solutions. I have been teaching my GeT course for four years. I hope to continue developing this course through my participation in the GeT community, so that it can better serve students’ various learning needs.

- What is your favorite book you have read in the last few years? I was very lucky to get a signed copy of Eugenia Cheng’s book The Art of Logic in an Illogical World at 2018 MathFest. I really like the way she connected mathematical ideas to social issues.
Did you get promoted? Win a grant? Have a baby? Buy a house? We would love to feature your news, whether professional or personal! Email us at GRIP@umich.edu.

Upcoming Events
How to Build Basic Logic on the Foundation of Mathematical Categories and Language
Friday, March 12 2:00 PM ET via Zoom
Friday, March 26 2:00 PM ET via Zoom

GeT Support
Sponsored by NSF DUE-1725837. All opinions are those of the authors and do not necessarily represent the views of the National Science Foundation or the University of Michigan.
Patricio Herbst, PI
Amanda Milewski, Co-PI
Get Support is housed in the GRIP Lab at the University of Michigan
Inese Berzina Pitcher, Project Manager
