
Table of Contents
- Illustrating a modeling approach to high school geometry: The pool problem by Patricio Herbst
- Reflecting on the SunRule as a Multiplication Model by Claudine Margolis
- The Geometry of Sunlight by Justin Dimmel
- GeT Course Student Learning Outcome #3 by Teaching GeT Working Group Members
- GeT Course Student Learning Outcomes #5 by Teaching GeT Working Group Members
- GeT Course Student Learning Outcome #9 by Teaching GeT Working Group Members
- Social Networks within GeT: A Pencil by Kolby Gadd
- GeT to Know the Community: Laura Pyzdrowski
- Transformation Working Group Update by Julia St. Goar
- Teaching GeT Working Group Update by Nat Miller
- Upcoming Events

Illustrating a modeling approach to high school geometry: The pool problem
by Patricio Herbst
This past March, I was invited to speak about high school geometry to a college geometry class, one that we might describe as a Geometry for Teachers (GeT) class insofar as future teachers were an important, even if not the only, constituency. I was asked to talk about why high school students need to study geometry—something that may be taken for granted in identifying geometry as a mathematics class that future teachers need to take but may make sense to ask from the perspectives of both college mathematics students and the mathematicians who teach them. In our proposal to NSF to fund the GeT Support project, we noted that contemporary mathematical research has little to do with the geometry content students learn in high school, and the same might be said about the mathematical experiences of undergraduates. Thus, if the geometry content does little to cement future learning or research, it is worth asking what role high school geometry plays in high school students’ mathematical development.
This question of the purpose of the study of geometry is not new. At the end of the 19th century, as the high school curriculum was being formed in the United States, the idea that different scholarly disciplines were useful to train different mental faculties was in vogue. Geometry was then justified on account that it was expected to train logical reasoning. González and Herbst (2006) describe this logical argument along with others which emerged later during the 20th century. An intuitive argument was offered that described geometry as providing a language that students could use to relate to their everyday experiences in the material world. A utilitarian argument was offered during the second world war period that described geometry as providing useful resources for the world of work. And during the time of the New Math (in the 1950s and 1960s) a mathematical argument emerged that described geometry as providing an opportunity for students to experience what mathematicians do: define, conjecture, prove, and so on (González & Herbst, 2006). To some extent those four arguments (logical, intuitive, utilitarian, and mathematical) are still being made in different quarters; furthermore, we may come by a better answer to the question by integrating some of those arguments. While the logical argument was questioned early in the 20th century, both the intuitive and the mathematical argument have always felt complementarily compelling to me.
A modeling approach
In my talk to that class in March, I proposed that the geometry course provides students with opportunities to engage in the mathematical modeling of their experiences with space and shape. Herbst, Fujita, Halverscheid, & Weiss (2017) used this idea as the centerpiece of their graduate textbook on the teaching and learning of geometry. They offered Figure 1 below as a way to represent what could happen in high school geometry. The box in the center represents an envisioned modeling approach to high school geometry. The approach is informed by two sets of sources. On the one hand there is a source that we could associate with the intuitive argument named above: Real world objects and activities are often represented (i.e., named, described, depicted) using tokens that might be described as geometric. So, words—like line, square, and turn—and shapes are often used in describing how people manage space and shape. This does not mean that by virtue of their use of those tokens those people are doing mathematics in a way commensurate with that of mathematicians, but an argument that builds on embodiment and materiality could be envisioned to suggest engagement in physical activities and their enactive representation has some mathematical qualities. The diagram in Figure 1 suggests that high school geometry could build environments on top of those existing relationships between the real world and our cultural representations of it. These environments are described as “geometric models of representations of real world objects” which means at least two things. On the one hand, these models are particular interpretations of the primitive objects, relationships, and postulates of formal geometries such as Euclidean geometry. On the other hand, these models are environments for mathematical practice—environments in which the activities (e.g., calculation, construction) and dispositions (e.g., pondering whether a solution is unique) of mathematical practice can be mobilized to produce information that can be interpreted in terms of real world objects and activities. The arrow from Geometries to these models and the adjective geometric attached to models point to the aspiration that work within those models be guided by the mathematical sensibility that reigns in mathematical practice. Teachers and curriculum developers who are likely to know geometry as a mathematical domain can organize these environments in which students’ experiences with real world objects and activities and their representations are involved in the activities of mathematical practice and scrutinized with the sensibilities of mathematical practice. A quick example of these relationships is the modeling role the use of a straightedge plays in helping think of a straight line when confronted with concrete objects that might be described as forming a straight line—questions of incidence, betweenness, separation, parallelism, and so forth can be brought from the geometric theory of lines and specific practices with the straightedge may help interpret those questions in terms of concrete objects. The famous quote by Poincaré, “geometry is the art of reasoning well from badly-drawn figures” (cited in Bartocci, 2013), comes to mind along with the common practice of drawing in geometric problem solving. A more detailed example may help make the point clearer.
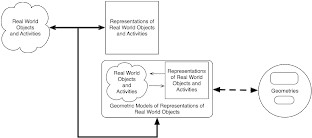
(adapted from Herbst et al., 2017)
The pool problem
The pool problem serves as a more extended example of the modeling approach. This problem could be used relatively early in the high school geometry course, after students have learned some basic constructions (e.g., how to construct a perpendicular bisector to a segment) and how to prove triangles congruent. The problem can be used to develop students’ knowledge of a theorem about right triangles: that, in any right triangle, the midpoint of the hypotenuse is equidistant from the vertices. More importantly, the problem can be used to inscribe in high school geometry a simple example of the mathematical difference between sense and reference (Frege, 1997/1892): The same mathematical object (the same point in this case) can be the referent of two different ways of speaking (two different meanings or senses). This notion is pervasive in mathematics as two different procedures can construct the same mathematical object. The pool problem can be used to instill the disposition to ask whether two different construction procedures define the same object.
The pool problem says
Three swimmers are going to jump into a rectangular pool and race toward a buoy. One of them will do so from a corner of the pool, a second from a side of the pool adjacent to that corner, and the third from the other adjacent side. Suppose the swimmers are in position and you have to position the buoy. Where should you position the buoy to make the race fair?
Note here that some geometric concepts are being used to describe the concrete situation: the pool is rectangular; the word adjacent is used to refer to the sides of the pool that make one of its right angles, etc. Finally, the notion that the race will be fair alludes to equidistance. That reading of the problem using geometry along with existing habits to study the geometry of the microspace (i.e., at a scale much smaller to that of the human body) might suggest an initial diagrammatic modeling to represent the problem: Students could draw a rectangle and plot three points for the swimmers. This initial modeling decision can be quite consequential in affording opportunities to project mathematical sensibilities onto the work; it can be advantageous, from a mathematical point of view, to have rectangles of different sizes and aspect ratios, rectangles drawn free hand, and rectangles constructed with straightedges. The expectation is that mathematical sensibilities and mathematical practice will help organize superficial variations among those representations. Poincaré’s proposition that “geometry is the art of reasoning well from badly-drawn figures” suggests that to reveal the geometry, it would be valuable if the diagram had some inaccuracies to begin with (such as the strokes representing the sides of the pool not being exactly straight or the angle representing the corner of the pool not being exactly 90 degrees; see figure 2).
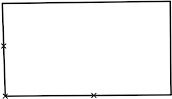
The drawing in Figure 2 represents the pool situation using geometry. Can students use it and what they know in order to make inferences about the situation? First of all, there are concrete answers that can be made available immediately: The distances between any point picked at will inside the rectangle can be measured with rulers, and the point may be moved so as to make the distances closer to each other. These answers can be revealed useless by virtue of the modeling choices: The distance that will be equal for one set of swimmer positions will not necessarily work for a different set of swimmer positions, and even if those positions were controlled, the particular measure of the distances among the points representing swimmer positions and prize location would unclearly prescribe how to locate the prize position in the actual pool. Thus, early modeling choices, using the tokens of intuitive geometry (vocabulary and imagery), might reveal the need for something else. In what follows I adopt the position of a teacher anticipating how one could think of the problem with a class: I consider my audience in terms of what they are expected to know (hence timing when and how I bring in what I know).
If we started from considering only two swimmers first, specifically the swimmer at the corner and a swimmer at one of the sides, it would be easy to see that the midpoint of the segment determined by the two swimmers is equidistant from them (and the pool context also suggests that would not be a reasonable place to locate the prize as such midpoint would not be in the pool!). But many other points in the pool would be equidistant from those endpoints. As students have learned to construct the perpendicular bisector of a segment, they might also know that this line is the locus of all points equidistant from the endpoints of the segment. And if they didn’t yet know that, this might be a good time for them to come to know it. It might help to ask questions like: Since the midpoint of the segment does not work, what would be a point inside the pool equidistant from the endpoints? Students might or might not bring the perpendicular bisector as a resource to think about other points. If they didn’t, one could ask how they would pick the point they are looking for, aiming to get explicit instructions. In our work with this problem in actual high school classrooms, we have seen students gravitate to the perpendicular bisector directly or to ideas germane to its construction (e.g., using the compass to make an arc from each of the endpoints and picking the point of intersection of the arcs). In case the students had thought of the perpendicular bisectors, the question, “how could we prove that a point chosen on the perpendicular bisector is equidistant from the endpoints?” might get to a partial conclusion of this simpler problem. In case the students had not thought of the perpendicular bisectors and instead constructed a single point, the question, “is there any other point that would work?” might move the discussion toward the end of characterizing all the points that would be reasonable locations for the prize.
Once that simpler problem has been solved, we can bring in the third swimmer. The ways of locating possible places for the prize in the simpler problem could help find possible locations for a prize that would be equidistant from the second and third swimmer. The question, “is there a spot that is equidistant from the first and the second swimmer and equidistant from the second and third swimmer?” could get students to think of the intersection between the two perpendicular bisectors. The question, “[how] do we know whether the first and the third swimmer are equidistant from the point of intersection of these two perpendicular bisectors?” is also relevant here and could bring awareness of the transitivity of congruence. In that event, we have found a solution to the problem, but we have not arrived yet at the statement of the theorem as no attention has been given to the midpoint of the hypotenuse; not even a right triangle is visible. Indeed, the midpoint of the hypotenuse and the intersection of the perpendicular bisectors of the legs of a right triangle are two different meanings (two different senses in Frege’s terminology) of the same referent. A virtue of this problem, and of this way of approaching the problem, is that it delays attention to the referent, making room, as we discuss below, for proof.
While one solution to the original problem has been proposed, it is mathematically sensible to ask whether that is the only one. Furthermore, the fact that we have found the one by doing some things with the diagram instead of others, it is also sensible from a diagramming action perspective to ask whether we would get a different point had we made other choices. In some cases, the question may yield simple, even trivial, answers, and in other cases, the question could lead to compelling stretches of mathematical practice. For example, if instead of considering first the two points on one side and second the two points on the other side, we altered that order, would the solution change? Students might be quick to note that the intersection of the same two perpendicular bisectors is a single point, no matter which perpendicular bisector is drawn first. The other possible choice is, or can be made to be, however, less immediate.
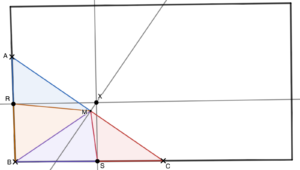
What if the first two points used for the simpler problem did not include a swimmer at the corner but were points on the sides of the pool? Because the segment determined by those two points has not been drawn yet, thinking about their perpendicular bisector might not be immediately obvious to students. The simpler problem warrants thinking about it, as the midpoint of that segment would be one reasonable place to position the prize if the swimmers jumped into the pool from the sides. One solution would be the midpoint of that segment. Yet, the real world situation also suggests some discomfort with it. In Figure 3, we can note that diving toward the midpoint of the segment between them would require swimmers to form an acute angle with the side of the pool and that it would feel more comfortable if that angle was larger. Thus, a practical reason might justify asking where, other than at the midpoint of the segment between the swimmers, are all the points equidistant to them. Based on what was considered in the first solution, students would likely gravitate toward thinking of the perpendicular bisector too, but this observation about the angle might importantly seed a preference toward a solution farther from the midpoint of the segment. Because we are not merely interested in solving the problem but in constructing the materials that matter in the theorem at stake (and more, as all of this matters in understanding why the circumcenter is unique), that preference is desirable; it helps create the conditions for students to understand that the referent of all these constructions is unique through rational means, by reasoning well about badly-drawn diagrams.
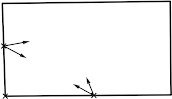
Now it would be reasonable to bring in the third swimmer, diving from the corner. Again, one could consider two different perpendicular bisectors. Considering only one would provide a solution but leave open the question of whether choosing the other perpendicular bisector would provide a different solution. Figure 4 shows what this could look like in a diagram deliberately chosen to favor the posing of these questions. A deliberately chosen, badly drawn diagram would be one in which one could see the three different meanings of the location of the prize (three different construction procedures) as if they pointed to three different referents.
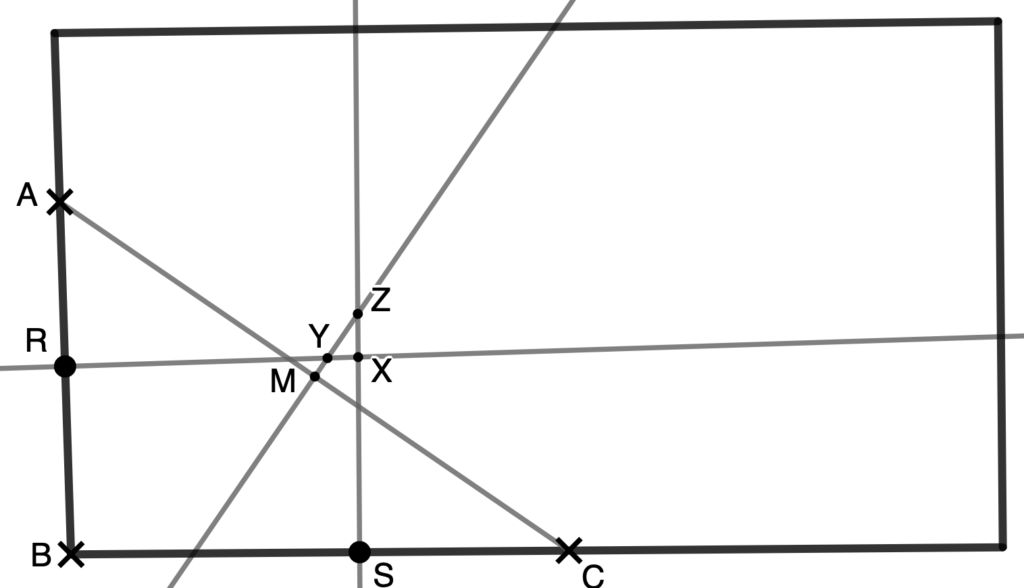
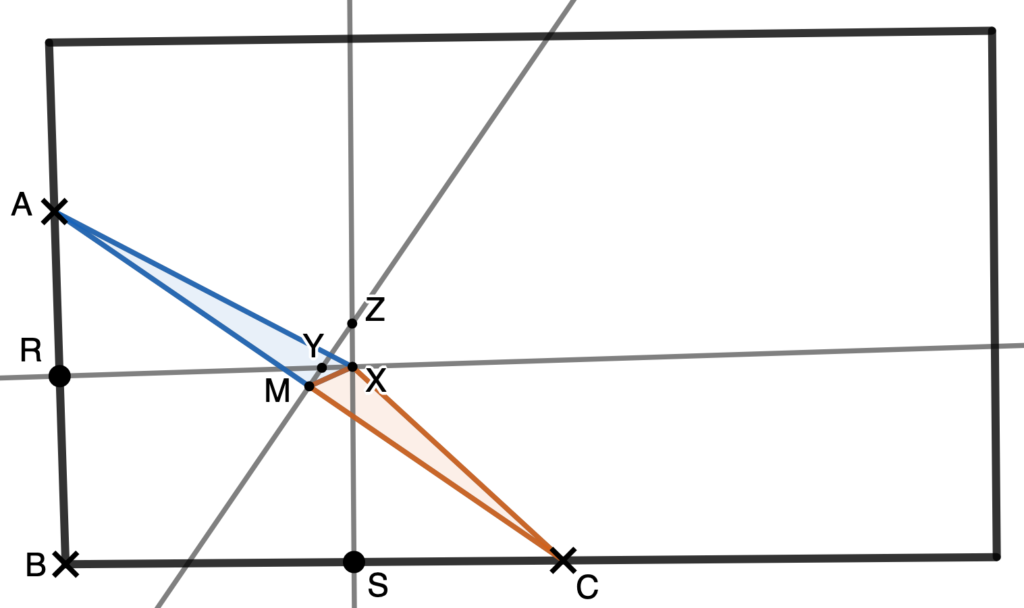
A superficial appraisal of figure 4a would avail the question, “are we saying that there are three different points equidistant from the three swimmers?” As the last two solutions were found on the perpendicular bisector of AC, the first point found (X; see Figure 4a) might appear as the odd one out and allow the questions: “Is X really equidistant from A and C? What would need to be true about triangles AMX and CMX if AX was congruent to CX?” If available, the reciprocal property of the perpendicular bisector (if a point is equidistant from two points, it is on the perpendicular bisector of the segment formed by the points) could come in handy to infer that X should be on the perpendicular bisector of AC. If not, the conclusion could be reached by noting that triangles AMX and CMX should be congruent by side-side-side (see figure 4b).
If not only Z and Y but also X are determined to be on the perpendicular bisector of AC, the students could be invited to draw the figure again, paying attention to locating X, Y, and Z. This is another case in which sense and reference are different; while one could talk about those as potentially different points, there would be no way of drawing them as distinct points that lie on a single line, even in a badly-drawn diagram!
However, one could still ask, “What about M?” If one now considers triangles, say BMR and AMR, they would need to be congruent by side-angle-side, making BM ≅ AM. Similarly, because BMS and CMS are congruent triangles, BM ≅ CM. This all would suggest M would also be in the intersection of all three lines and the only point that can be used to place the prize. X, Y, Z, and M would be one and the same point.
Back to the modeling approach
Badly drawn diagrams, such as those in Figures 4a, 4b, and 5, are doing things that formal, axiomatic geometry cannot do. By offering a diagrammatic interpretation of geometric concepts and relationships, they activate a source of intuitive feedback to the questions, assertions, and predictions that may come from the mathematical sensibility. This mathematical sensibility is one capable of endowing a badly drawn diagram with some properties and looking for it to produce other possible properties. This mathematical sensibility is one that will be ready to question the consistency of both classes of properties; and it is essential in order for reasoning with diagrams to model mathematically the relationships between real world objects and activities (including the activities of drawing, folding, and moving about in space) and the geometric representations of those objects and activities. As the narration above suggests, for the high school geometry class to have access to that mathematical sensibility not only well-chosen tasks are needed but also a teacher who is disposed to both ignore publicly what they know about geometry while embodying the dispositions to know that are part of the mathematical sensibility. In such a context, one could see the high school geometry class as a place where students are apprenticed into the practice of mathematicians by working with the intuitive ideas of geometry. High school geometry could be the place in which one learns to resolve the logical contradictions that arise from drawing bad diagrams and thinking with badly drawn diagrams. This modeling approach builds on earlier arguments for why students should study geometry. The importance of engaging in the practices of mathematicians is affirmed as a way to solve problems by making representations whose attributes are ascribed and verified rationally as opposed to empirically. Geometric content is valuable not because geometry is a preferred example of a mathematical system of postulates, theorems, and proofs, but because experiences managing space at different scales provide sources for representations (embodied, iconic, symbolic) that can help pose problems and provide feedback on thinking. Logical reasoning is called upon to support mathematical practice, as well as to confront the feedback from various representations. And the capacity to mathematically model experiences with shape and space, while contextualized in geometry, might support modeling in work contexts, where it can be useful to anticipate rationally the solutions to problems of managing space and shape.
References
Bartocci, C. (2013). “Reasoning well from badly drawn figures”: the birth of algebraic topology. Lettera Matematica, 1(1-2), 13-22.
Frege, G. (1997). On Sinn and Bedeutung In M. Beaney (Ed.), The Frege reader (M. Black, trans., pp. 151-171). Blackwell. (Original work published 1892)
González, G. and Herbst, P. (2006). Competing arguments for the geometry course: Why were American high school students supposed to study geometry in the twentieth century? International Journal for the History of Mathematics Education, 1(1), 7-33.
Herbst, P., Fujita, T., Halverscheid, S., and Weiss, M. (2017). The learning and teaching of secondary school geometry: A modeling perspective. New York: Routledge.
Suggested Citation
Herbst, P. (2021, May). Illustrating a modeling approach to high school geometry: The pool problem. GeT: The News!, (2)3. https://www.gripumich.org/v2-i3-s2021/#illustrating-a-modeling-approach-to-high-school-geometry-the-pool-problem

Reflecting on the SunRule as a Multiplication Model
by Claudine Margolis
At the February GeT Seminar, Justin Dimmel made a compelling case for the use of light from the sun and stars as a naturally occurring context to study the geometry of parallel lines. One outcome of his work has been the ongoing development of a mathematical tool called the SunRule. By combining the geometry of parallel lines which model the sun’s light, the mathematics of proportionality in similar figures, and the functionality of a slide rule, the SunRule allows the user to calculate the product of two quantities. Justin prompted us to consider the way this new tool could be used for mathematics teaching and learning, including teaching and learning for preservice mathematics teachers. I was interested in exploring the potential conceptions of multiplication that might arise from using the SunRule for computing products and making sense of multiplication, so I created a virtual version on Desmos for experimentation.
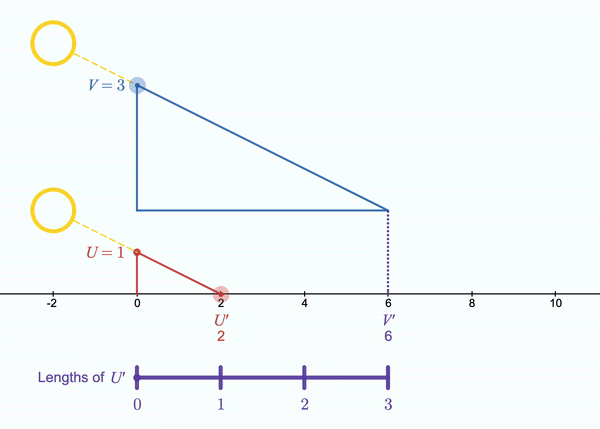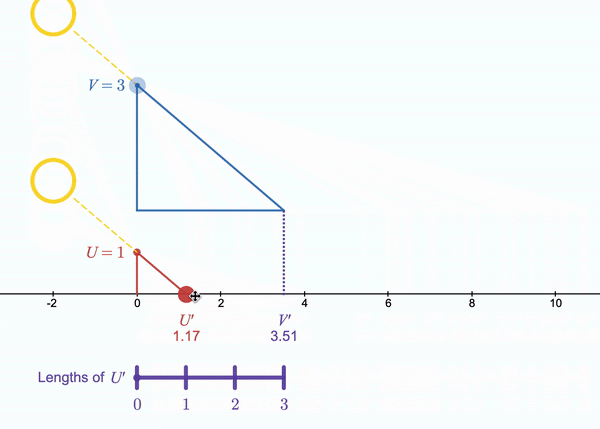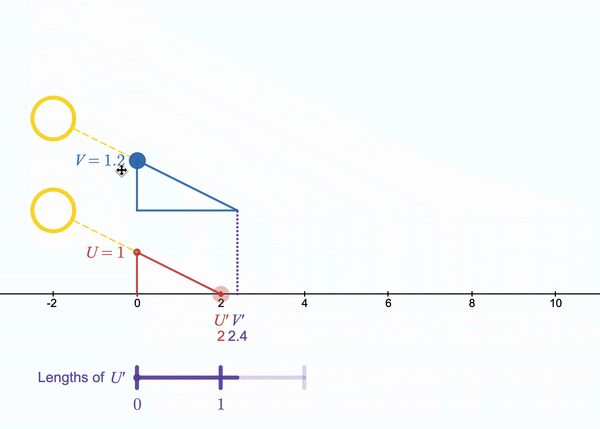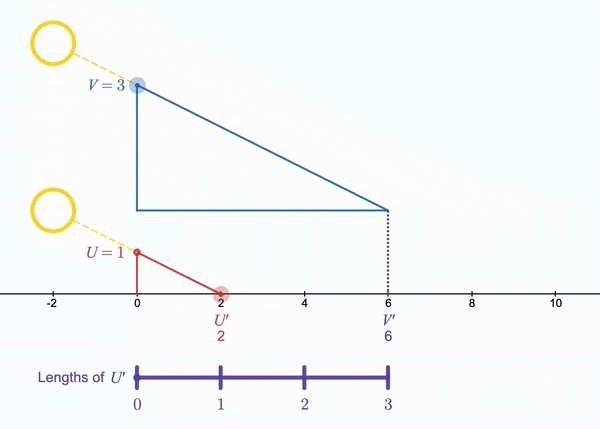
The SunRule leverages parallel light rays from the sun to create shadows along a ruled board. The shadows are cast by two gnomons, one (U) which is a single unit tall and the other (V) which can be set to any length (within the physical constraints of a physically instantiated SunRule). By tilting the board with gnomons attached, the angle (θ) at which the shadow “intersects” the board can be adjusted. The length of the shadow that the unit gnomon projects (U’) onto the board can be adjusted in this way, resulting in a proportional adjustment of the length of the shadow projected by the gnomon of variable height (V’).
The SunRule can be used to calculate the product of a • b by setting the height of V to a length of a and adjusting the angle of the board so that the length of U’ is b. The value of the product can be read as the length of V’, or the distance that the shadow of the variable length gnomon reaches along the ruled board. A series of products are illustrated in Figure 1.
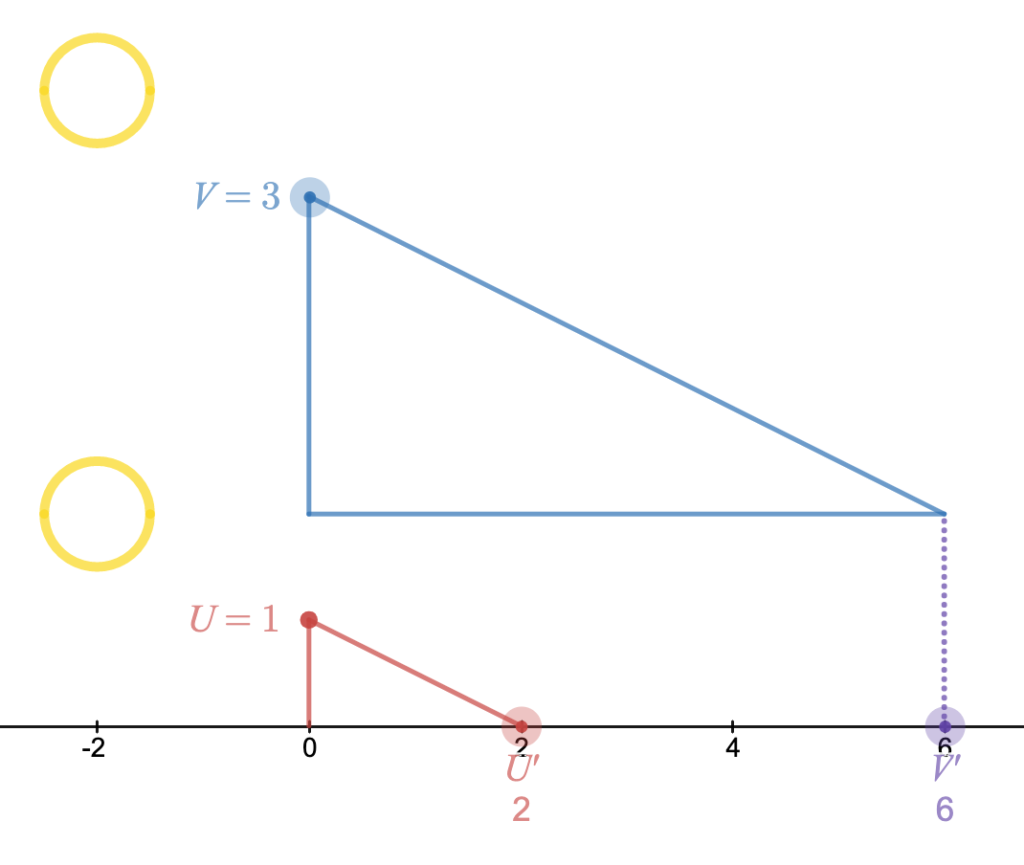
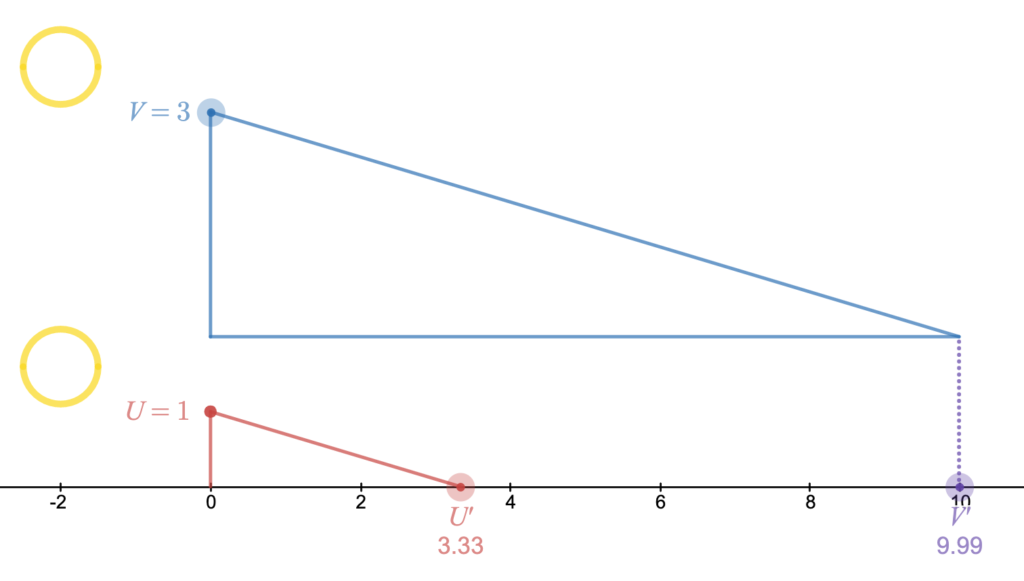
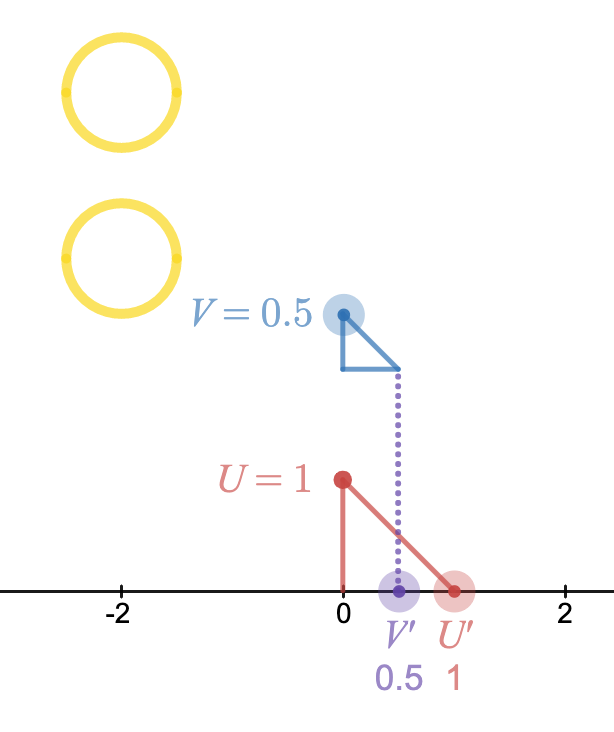
Figure 1. Three SunRule states that illustrate the product of two values.
Once I understood how the SunRule could be used to compute products, I started to wonder what we can learn about multiplication with this model. My interpretation of the SunRule is that it scales the quantity U’ by a factor of V (as shown in Figure 2), although others might interpret it as the quantity V being scaled by a factor of U’. If both factors are integers, the product can be interpreted as V groups of the length U’ (as illustrated by the purple bars at the bottom of Figure 2), but the variable length gnomon can be set to any value between 0 and some maximum determined by the length of the rod being used. There is no reason for it to be set to an integer value. What happens if we set it to a non-integer value? What happens if we set V<1? What if we set U’<1? What if either factor is 0? What if either factor is negative? What if both factors are negative? What happens to the product as one factor slides continuously? What if both factors slide? If one factor is increasing at the same rate the other factor is decreasing, what happens to the product? What does the area of each triangle represent?! I would argue that many of these questions are best answered by playing with the SunRule eTool rather than considering static examples, though Justin might argue that playing with a real SunRule is even better than playing with an eTool. For now, sharing the eTool is easier than sharing the real thing, so try it for yourself: https://www.desmos.com/calculator/fj7zbbrkrd
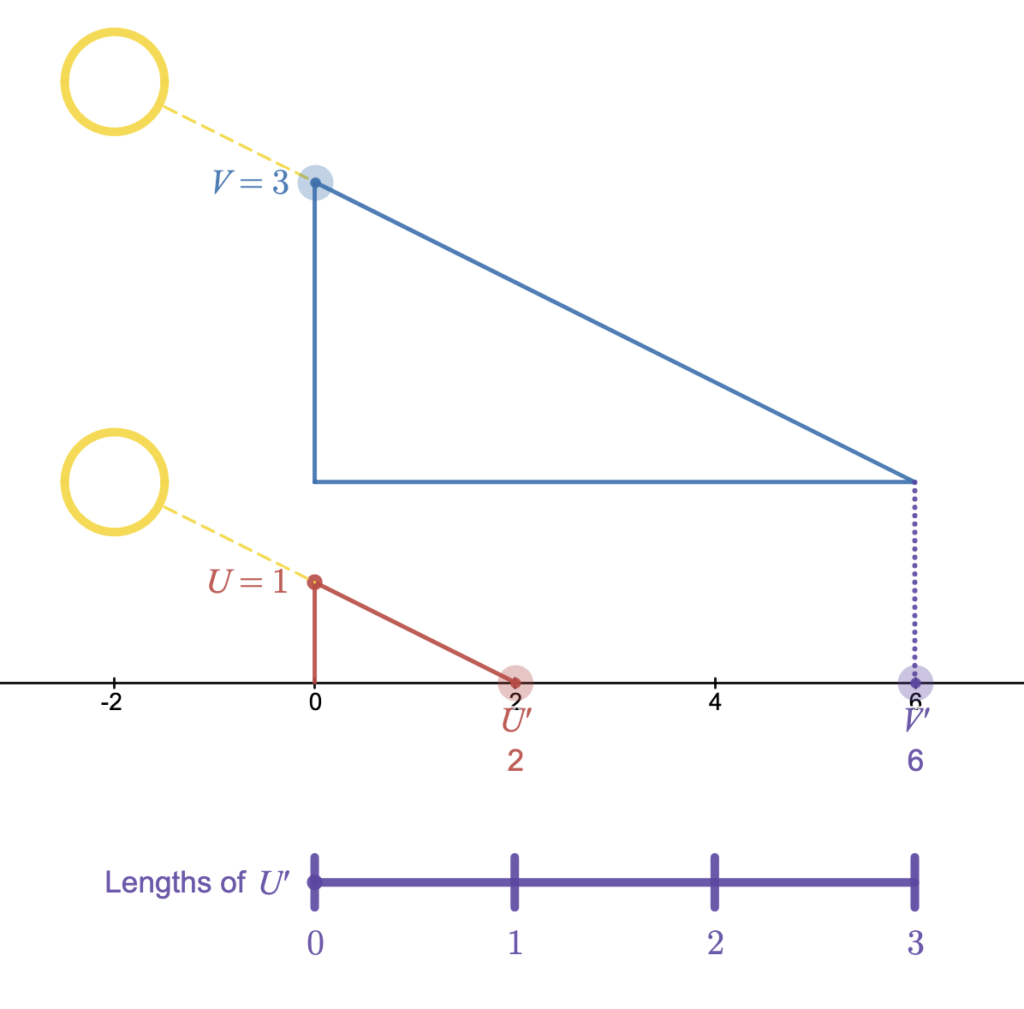
What I have found most interesting is the relationship between the purple bar at the bottom of the diagram (let’s call that a U’ Number Line) and the horizontal axis which measures lengths of U. As we let U’ slide, the U’ Number Line is stretched or compressed, but the number of units displayed remains constant. As we let V slide, the length of a unit remains constant, but the number of units displayed changes. If we focus on the relationship between the U’ Number Line and the horizontal axis, we have a new (to me) representation of a double number line that can model multiplication of two continuous variables. It feels very similar to the classic number line representation of multiplication, which models a • b as a “jumps” of b length along a number line, but we no longer need to limit a to being an integer.
I invite you to play with and think about what the SunRule makes available for students to learn about multiplication. What does it obscure? What does this virtual approximation of the SunRule make available that the real SunRule does not? What does it obscure?
Suggested Citation
Margolis, C. (2021, May). Reflecting on the SunRule as a Multiplication Model. GeT: The News!, (2)3. https://www.gripumich.org/v2-i3-s2021/#reflecting-on-the-sunrule-as-a-multiplication-model

The Geometry of Sunlight
by Justin Dimmel
Sunlight provides an abundant, renewable, accessible source of naturally occurring rays that, for all intents and purposes, are parallel. It is the rare example of a real-world context with which nearly all children are familiar. Despite its familiarity and near universality, sunlight plays almost no part in K-12 mathematics classrooms. This is a missed opportunity in geometry classrooms in particular, where sunlight could provide not only an exemplification of the Euclidean notion of parallel lines but also raw material for doing mathematical work. This note explores the parallelism of sunlight and proposes a collaborative activity that would recreate an ancient geometric triumph: Eratosthenes’ measurement of the circumference of the Earth.
On the parallelism of sunlight
Eratosthenes of Cyrene was the chief librarian at the library of Alexandria during the 3rd century BC. Popular retellings of Eratosthenes’ method for measuring the circumference of the earth tend to dwell on the assumption that sun rays are parallel. For example, a recent (2019) article in Medium describes this assumption as, “incorrect, but acceptable for the equipment available at the time.” It is true that Eratosthenes made an assumption about sunlight, but to dismiss this as something that was harmless but ultimately incorrect elides an opportunity for mathematical investigation.
The parallelism of sunlight can be understood in comparison to a more familiar real world example of parallel lines: railroad tracks. For high-speed rail, the gauge variation, or the allowable variation in the distance between tracks, as measured along any 3m length of railway, must not exceed 6mm. Thus, railroad tracks are permitted to deviate from parallel by nearly 7’ of arc (where 1’ of arc is 1/60 of a degree):
tan-1 (6/3000) = .1145 degrees = 6.87’ of arc
This is the angle that is subtended by one 3m (3000mm) length of track and the 6mm tolerance. By contrast, the deviation from parallel of sunlight over a distance of 3m is effectively zero, because Earth is nearly 150 billion meters from the sun:
tan-1 (3/150,000,000,000) = .000000001 degrees = .00000006’ of arc
Thus, locally, sun rays are not only more parallel than railroad tracks, their deviation from parallel is well below the threshold of what can be measured with a theodolite. Even globally, sunlight’s deviation from parallel is all but negligible:
tan-1 (6,500,000/150,000,000,000) = .0025 degrees = .15’ of arc
So, it is technically true, in a narrow sense, that sun rays striking the Earth are not parallel. But practically, effectively, sun rays are parallel, and this parallelism is a resource that can be harnessed for doing mathematical work.
The solstice, the cities, and the well
Apart from a concern about the parallelism of sun rays, other legacies of the legend of Eratosthenes are the significance of the date—the measurements are said to have occurred on the summer solstice, the locations of the cities in which the measurements were taken—Syene and Alexandria, and the well that was said to perfectly reflect the noon sun. Narratively, these details add richness to the story that help to situate the measurement as a historically significant achievement that was a product of the ancient world. And it was all those things. However, mathematically, these details bury the lede, which is that the parallel rays of the sun allowed a surface dweller to measure the size of the very earth under his feet; because the sun’s rays are parallel, any observed differences in the altitude of the sun must be a result of the curvature of the earth. Thus, by comparing the altitude of the sun at different locations, it is possible to deduce the size of the earth. The date, the locations, and the well are immaterial. The measurements could take place on any day, anywhere, provided the different places where the measurements take place are not too close together. To recreate the feat, all that is needed is coordination—of the date on which to make the measurements—and improvisation—of a device for measuring the altitude of the sun.
Here is how it would work:
- We choose a date to take the measurements. This could be before the end of the academic year or else in the late summer or early fall, as an activity that could kick off the next academic year.
- We engineer devices that can measure the maximum altitude of the sun. The image below (Figure 1) shows an example of one such device, improvised from a phone, a shoe, a pencil, a rubber band, and graph paper.
- We compare our measurements against the north/south displacement of where the measurements were taken. For example, if measurement locations are near odd-numbered interstate highways, it may be possible to approximate the north/south displacement from mile markers.

The device shown in Figure 1 is designed to record the shadows cast by a gnomon as the sun moves across the sky near local apparent noon. The pencil acts as a gnomon, which is the technical name for the part of a sundial that casts a shadow. The shadow of the gnomon is projected onto graph paper, which allows for the calculation of the apparent altitude of the sun (using the height of the gnomon off the ground, the length of its shadow, and the arctangent relationship). Finally, the apparatus is mounted to a phone, so that the movement of the shadow around solar noon could be recorded. When the shadow reaches its shortest length, the sun attains its highest altitude, and that is the measurement that would be used for the activity. This is intended only as an example of a device that could be improvised; readers are encouraged to use their own design and engineering skills to create something better.
This is a sketch of a plan that will be hashed out in more detail among the group of readers (and their students!) that want to participate in this collaborative recreation of Eratosthenes’s feat. If you would like to participate, please email me (on or before Monday, June 7) at justin.dimmel@maine.edu. I will email those who express interest, and we will come up with a plan that works for everyone who wants to be involved.
References
Decamp, N., & Hosson, C. (2012). Implementing Eratosthenes’ discovery in the classroom: Educational difficulties needing attention. Science & Education, 21(6), 911-920.
Suggested Citation
Dimmel, J. (2021, May). The Geometry of Sunlight. GeT: The News!, (2)3. https://www.gripumich.org/v2-i3-s2021/#the-geometry-of-sunlight

GeT Course Student Learning Outcome #3
by Teaching GeT Working Group Members
SLO 3: Secondary Geometry Understanding. Understand the ideas underlying the typical secondary geometry curriculum well enough to explain them to their own students and use them to inform their own teaching.
While there are students who do not plan to teach geometry in Geometry for Teachers (GeT) courses at most institutions, it is required for those who will become secondary math teachers. To be a good secondary geometry teacher, one must understand the content, know the best practices for teaching the content, and be able to reflect on one’s teaching.
Although high school geometry is described as “devoted primarily to plane Euclidean geometry, studied both synthetically (without coordinates) and analytically (with coordinates)” (NGA & CCSSO, 2010, para. 2), for many reasons, students in the U.S. often enter a GeT course with varying levels of knowledge of Euclidean geometry. As GeT instructors, it is our job to fill in the students’ knowledge gaps so they are prepared to teach secondary geometry. However, due to limited time in a GeT course (usually one semester) and GeT instructors’ varied preferences in content selection, it is not practical to suggest a list of geometry topics to be covered in a GeT course. Thus, the GeT course should focus on helping students understand essential mathematical practices and develop problem-solving skills that can be translated to any geometry topic.
The Standards for Mathematical Practices are the most important piece of the Common Core State Standards for Mathematics (CCSSM), which “describe varieties of expertise that mathematics educators at all levels should seek to develop in their students” (NGA & CCSSO, 2010, para. 1). Even though some states have moved away from using CCSSM and have developed their own state standards, their new state standards typically include these eight practices or something similar to them. These practices form the foundation for good mathematics teaching. They are:
- Make sense of problems and persevere in solving them.
- Reason abstractly and quantitatively.
- Construct viable arguments and critique the reasoning of others.
- Model with mathematics.
- Use appropriate tools strategically.
- Attend to precision.
- Look for and make use of structure.
- Look for and express regularity in repeated reasoning. (NGA & CCSSO, 2010)
Furthermore, these practices provide the structure for mathematical problem solving, and any GeT student can benefit from becoming a better problem solver. We also want pre-service secondary geometry teachers to be able to model these practices in their future classrooms so GeT instructors should model these in our own classrooms.
All GeT instructors need to be aware of teacher preparation standards that have been created to help prepare secondary geometry teachers (Table 1) and to incorporate them in their GeT course designs in a way that fits their teaching agenda. Many different professional organizations (e.g., AMTE and NCTM) contributed to these standards and suggested what faculty should be doing to prepare better secondary mathematics teachers. GeT instructors should also be aware of the national and state curriculum standards (Table 1) and introduce them to GeT students so that they can start to become familiar with the standards that they will teach. The majority of states in the U.S. have adopted the CCSSM for their K-12 schools (see this map), and if your state does not use CCSSM, it is best to Google “State K-12 Mathematics Standards.”
Table 1
Resources for Standards
[table id=1 /]Because GeT courses are required for students who will become secondary mathematics teachers, GeT instructors must understand the needs of this group of students when in their course. It is not enough for these students to know the content, these students must gain specialized knowledge to teach effectively. Shulman (1986) describes this as pedagogical content knowledge; it includes, in part, an understanding of what makes learning some topics easy or difficult. To have this type of understanding, students must have opportunities to reflect upon and compare/contrast analogies, illustrations, and examples. Ball, Thames, and Phelps (2008) describe pedagogical content knowledge as a bridge between content knowledge and the practice of teaching. GeT instructors should foster the construction of this knowledge by sharing teaching techniques and through conversations about teaching geometry content. For example, by taking the time to discuss multiple approaches to solving problems or by examining different frameworks for writing proofs, the GeT instructor is providing students the opportunity to reflect on misconceptions and ways that make the content more understandable by others. This type of knowledge is necessary for future teachers.
Another aspect that helps with secondary geometry understanding is technology. Many teacher education standards and curriculum standards have addressed the use of technology in some way. For example, one of the grade 8 CCSSM geometry standards specifically mentions geometry software. Therefore, the GeT course needs to utilize technology to help understand and explore concepts in geometry. More information about the use of technology will be addressed in the Technology SLO.
References
Ball, D. L., Thames, M. H., & Phelps, G. (2008). Content knowledge for teaching: What makes it special? Journal of Teacher Education, 59(5), 389–407.
National Governors Association Center for Best Practices [NGA], & Council of Chief State School Officers [CCSSO]. (2010). Common Core State Standards for Mathematics. Available at http://www.corestandards.org/Math/
Shulman, L. S. (1986). Those who understand: Knowledge growth in teaching. Educational Researcher, 15(2), 4-14.
Suggested Citation
An T., Boyce, S., Cohen, S., Escuadro H., Krupa E., Miller N., Pyzdrowski L., Szydlik S., & Vestal S. (2021, February). GeT Course Student Learning Outcome #3. GeT: The News!, 2(3). https://www.gripumich.org/v2-i3-s2021/#get-course-student-learning-outcome-3

GeT Course Student Learning Outcomes #5
by Teaching GeT Working Group Members
SLO #5 [Definitions] Understand the role of definitions in mathematical discourse:
- Understand the importance of precise definitions for geometric objects andthat necessarily some geometric terms and relationships must remain undefined.
- Recognize that there are a variety of acceptable definitions for some geometric objects.
The role of definitions in mathematics is a rich area for students’ exploration that is often overlooked. In many math classes, definitions are given by the textbook or teacher. However, in a geometry class, definitions can be a fruitful area for students to explore. Students can propose their own definitions for elementary concepts, such as a square, a triangle, circle, or even a straight line. They can engage in class discussions about verifiable mathematical definitions versus vague descriptive definitions, and they can compare and contrast definitions with different properties included. For example, when asked to define what a rectangle is, one student might say it is a quadrilateral with four equal angles; another might say it is a quadrilateral that has at least three right angles and doesn’t have four equal sides; another might say it is a quadrilateral with reflection symmetry across the perpendicular bisectors of its sides; yet another might say it is a quadrilateral with four congruent angles and two pairs of congruent parallel sides.
Classes can have rich discussions regarding both the equivalence and the quality of proposed definitions. Criteria for the quality of definitions could include: (1) use of commonly understood words or previously defined terms, (2) accurately describing what is being defined, and (3) including no superfluous information. One strategy to convey the need for (1) is to “define” two “nonsense” words with definitions that refer to one another and hence have no meaning. Some definitions must involve undefined terms, to avoid infinite regress. A strategy to convey this is to ask students to come up with a definition of a familiar object and prompt them to define the terms they use in their definition.
Choices for definitions necessarily set the context for proving activity. For example, proving that two lines are parallel because they do not intersect can be very different from proving that they are parallel because they are everywhere equidistant. GeT students can also consider how changes in the assumptions within a geometric definition can lead to changes in the interpretations of other terms involving that definition. For example, a circle is often defined as the set of all points in a plane that are equidistant to a given point. If a geometry adopted the Euclidean metric for distance, then the property that distinct circles have a finite number of intersections holds; however, this property is not maintained with the Taxicab metric (Krause, 1975).
The logical consequences of statements involving a definition include the assumed meanings for terms within a definition as well as the axioms of the system . For those who include significant non-Euclidean topics there is opportunity to investigate the same definitions using different models. For example, there are no quadrilaterals with four right angles on the surface of the sphere or on the hyperbolic plane, but there are still quadrilaterals with reflective symmetry over the perpendicular bisectors of their sides. On the hyperbolic plane, there are lines that do not intersect but are not everywhere equidistant. On the sphere, there are not any lines that do not intersect, but there are still lines that make equal corresponding angles with a transversal. Some instructors have been surprised to discover that when students spend time in class exploring definitions and then are given a new space to explore on their own, they can productively spend weeks exploring the implications of potential definitions. For instance, what is a circle on the surface of a cone? If a circle is defined as the set of all points obtained by going a fixed distance from a given center in all directions, we get different circles than if a circle is defined as a figure with constant curvature, which is in turn different than if a circle is defined as a closed figure such that every straight line segment from the center to the boundary is the same length. Each of these types of circles have different properties that students can explore.
The taxonomy of geometric objects is closely tied to definitions, and the exercise of classifying objects helps GeT students attend to the ramifications of adopting different definitions and become prepared to support prospective students’ reasoning at different Van Hiele levels (see, e.g., Burger & Shaughnessy, 1986). In elementary school, students are taught how to identify and classify different quadrilaterals as rectangles, rhombi, squares, or none of the above. As definitions become formalized in middle and high school geometry, they become associated with increasingly generic representations. It is in the GeT course that students consider the results of adopting alternative definitions for geometric terms. For example, trapezoid is typically defined inclusively in college geometry courses (a trapezoid is a quadrilateral with at least one pair of parallel sides) but it is sometimes defined exclusively in elementary and secondary courses (a quadrilateral with exactly one pair of parallel sides). Other terms commonly encountered in secondary geometry for which GeT students could discuss the consequences of adopting definitions supporting exclusive or inclusive meanings include: whether coincident lines are types of parallel lines, whether kites are types of rhombi, and whether the identity transformation is considered to be a type of rotation or a type of translation. Determining whether and when definitions have equivalent meanings and the consequences of adopting exclusive or inclusive definitions prepares GeT students for the varieties of geometric definitions they may encounter in teaching secondary geometry.
References
Burger, W. F., & Shaughnessy, J. M. (1986). Characterizing the van Hiele levels of development in geometry. Journal for research in mathematics education, 17(1), 31-48.
Krause,E. F. (1975). Taxicab Geometry. Addison-Wesley Publishing. Menlo Park, CA.
Suggested Citation
An T., Boyce, S., Cohen, S., Escuadro H., Krupa E., Miller N., Pyzdrowski L., Szydlik S., & Vestal S. (2021, February). GeT Course Student Learning Outcome #5. GeT: The News!, 2(3). https://www.gripumich.org/v2-i3-s2021/#get-course-student-learning-outcome-5

GeT Course Student Learning Outcome #9
by Teaching GeT Working Group Members
SLO 9: Non-Euclidean Geometries. Compare Euclidean geometry to other geometries such as hyperbolic or spherical geometry.
Just as visiting another country can offer us a richer perspective on our own culture, so too can the study of non-Euclidean geometries help students to develop a deeper understanding of Euclidean geometry. While it is natural for students to be uncomfortable working in a geometry that varies from their intuition, non-Euclidean geometries afford an opportunity to explore and visualize novel worlds that can engage their imagination. In addition, learning the rules of these geometries puts students that plan to teach in the position of their students who may be learning Euclidean geometry for the first time. The choice of which different non-Euclidean geometries to consider might depend on the demands of the GeT course, but all offer new perspectives on familiar geometric objects and relationships.
In our everyday experience we regularly encounter multiple geometries. Buildings tend to be Euclidean. We expect floors and ceilings to be planar. Outside, the horizon reminds us that we live on a sphere. Our visual field routinely processes distant objects as smaller than comparably sized things that are nearby, just as they could be represented in projective geometry. In the car, we measure distance with a taxicab metric. Fans of science fiction may even encounter images and ideas of hyperbolic geometry. Notably, non-Euclidean geometries can be viewed through two different lenses: geometrically, as spaces that are physically different from Euclidean space, or axiomatically, as spaces in which different axioms are true.
The amount of time devoted to non-Euclidean geometries can vary widely depending on factors including audience, instructor preference, and institutional expectations. For a class consisting primarily of pre-service teachers, a substantial amount of Euclidean content is necessary, though at least some non-Euclidean geometry is recommended. In a comparative geometries course it would be natural to consider several different non-Euclidean geometries, while a class that focuses primarily on Euclidean geometry might include a brief survey of some non-Euclidean examples or focus on one flavor for a longer period of time. In any case, what follows are some of the learning opportunities offered by each.
Incidence Geometries are useful for getting a sense of how theorems follow from a set of axioms. These involve a reduced set of axioms and perhaps make it easier to introduce some principles of proof writing in that context. Taxicab geometry is an easily described alternate geometry that can lead to rich mathematical exploration. Here we note that when we speak of “non-Euclidean geometry,” we mean this broadly, referring to geometries that are different from our usual notion of Euclidean two-or three dimensional space. In taxicab geometry, we change our usual definition of distance in the plane. Rather than using a Pythagorean measurement, we measure the distance between two points as the sum of the absolute differences of their Cartesian coordinates. This radically changes the form of objects that are defined in terms of distance. For example, a circle (the set of points at a given distance from a given point) no longer appears round. Ellipses, hyperbolas, and parabolas provide an even greater challenge!
Spherical geometry offers the advantage of being (fairly) easy to visualize (or hold in your hand). As a more accurate representation of the surface of the planet than a flat Euclidean world, it has relevance. An introduction to spherical geometry immediately challenges our understanding of the undefined term “line” and our belief that between any two points there can be drawn a unique line. Other explorations might have students consider parallel lines on the sphere or the angle sum of a triangle.
Taxicab and spherical geometry serve well as examples of non-Euclidean geometries that can be explored at any point in a GeT course. Hyperbolic geometry can be as well, though its close relationship to Euclidean geometry is perhaps best appreciated when students are more experienced with axioms and axiomatic systems. Hyperbolic geometry differs from Euclidean geometry only in a parallel postulate. In Euclidean geometry, we assume there is exactly one parallel through a given point not on a given line. In hyperbolic geometry, we adopt a different parallel postulate, so that there are multiple lines through a given point parallel to a given line. Changing this axiom is, in fact, how hyperbolic geometry was first developed historically. Moreover, we can simply remove that axiom altogether to end up with a third geometry, Neutral geometry. Comparing the mathematical properties of these three geometries and their interplay leads to rich discourse. It is also worth noting that although hyperbolic geometry perhaps arises most naturally from this axiomatic change, it can also be viewed geometrically as a space of constant negative curvature. In this sense, it provides an instructive example of a non-Euclidean geometry having properties different from Euclidean geometry.
The relationship between Euclidean, hyperbolic, and Neutral geometry can be made explicit by proving the equivalence of parallel postulates in Neutral geometry. For example, transitivity of parallelism (“Two distinct lines each parallel to a third line are parallel to each other.”) is logically equivalent to Euclid’s fifth postulate in Neutral geometry. Proving that equivalence, or one similar, can be a valuable experience by strengthening student understanding of proof. These proofs are demanding but are generally relatively brief.
Rectangles (quadrilaterals with four right angles), for example, are among our most familiar geometric objects. However, while the existence of rectangles can be easily established in Euclidean geometry, it can be proven that they exist neither in hyperbolic geometry or in spherical geometry. In both of those cases, a pair of lines can share at most one common perpendicular line making a rectangle impossible. In Neutral geometry, we can neither prove nor disprove their existence. Likewise, we can show that similar, non-congruent triangles do not exist in hyperbolic geometry. Examples such as these differentiate between the geometries and demonstrate the necessity of Euclid’s fifth postulate. In this way, they can help strengthen student understanding of axiom systems.
Hyperbolic geometry offers opportunities for students to strengthen their facility with geometric straightedge and compass constructions through an exploration of hyperbolic geometry models. Since both the Poincaré and Klein models of hyperbolic geometry are situated within Euclidean geometry, constructions of “lines” and “perpendiculars” in these models translate to Euclidean constructions. These constructions can cover a range of complexity, from the trivial (e.g., constructing a “line” in the Klein disk) to the highly involved (“Dropping a perpendicular” in the Poincaré disk). Dynamic geometry software is an excellent resource here, as there are a wealth of online tools available that automate some of the most difficult constructions. This has the added benefit of encouraging students to engage in higher order thinking on constructions in ways that were not possible only a few years ago.
Suggested Citation
An T., Boyce, S., Cohen, S., Escuadro H., Krupa E., Miller N., Pyzdrowski L., Szydlik S., & Vestal S. (2021, February). GeT Course Student Learning Outcome #9. GeT: The News!, 2(3). https://www.gripumich.org/v2-i3-s2021/#get-course-student-learning-outcome-9

by Kolby Gadd
We all know the past many months have presented challenging circumstances to do our work. Facing these challenges underscores the importance of personal and professional social networks to maintain one’s connection, productivity, and wellbeing. During the COVID-19 pandemic, CEDER, the organization contracted to do evaluation work on behalf of GeT Support, has used social network theory (see, e.g., Borgatti & Ofem (2010) and Portes (1998)) to learn about the experiences members of GeT: A Pencil have had in the group. My purpose here is to share some of the findings from our analysis.
Our analysis relied on data collected from a survey and interviews with members of GeT: A Pencil. Our survey included questions about group interaction and the activities they did together. In total, 18 of 29 members of GeT: A Pencil responded to our survey. These members generally had high levels of experience both as teachers of GeT courses and as members of GeT: A Pencil. Half of all respondents reported having taught a GeT course more than five times in their career. Also, more than half joined GeT: A Pencil at least two years ago.
To complement the survey data, we also interviewed members of GeT: A Pencil to learn more about their thoughts and experiences regarding activities and relationships within the network. We asked participants, for example, about ways their thinking about teaching has evolved as a result of participating in the network and how the network could be more supportive of their work as GeT instructors. We invited people for interviews who would help us understand the range of experiences within GeT: A Pencil, and CEDER staff interviewed 16 of 29 GeT: A Pencil members.
When asked about benefits of being a member of GeT: A Pencil, most respondents discussed the interactions they have had with other community members. One member shared about opportunities to interact with others who have a wide range of expertise saying:
“I feel like there’s lots of things happening all the time with [the community]. There’s a seminar I could sit in on, a group of people that are working on different issues that are national issues…I think one of the big strengths of the community that they’ve developed is the breadth. There are lots of different things that people are working on. Lots of different people that I could talk to if I have a particular question about a topic that I want to maybe change a little bit in my class, or maybe do something a little different next time. I have people that I could reach out to that I wouldn’t know about otherwise. There was not another place that I would be able to find out who’s doing something interesting or cool or intriguing in college geometry classes.”
This quote illustrates the quality of connections available to members of GeT: A Pencil. Survey responses also provided evidence of the breadth of activities that promoted connection among members. Analysis showed, for example, that members who reported reading the newsletter, using instructional resources shared within the network, and attending working group meetings formed connections with others that helped them reflect on their work as instructors in GeT courses.
Interviews provided further evidence that many relationships among members of GeT: A Pencil are supportive of members’ work as instructors. In interviews, respondents described changes to their teaching that they attributed to their participation in GeT: A Pencil. Eleven of the fourteen people who responded to this question reported they have changed or plan to change their teaching practices as a result of engagement with the community. Members reported they have changed their pedagogy to better facilitate conversations with students, make the course more interactive, or engage students in more problem-based learning. One member changed how they taught proof based on ideas they got from the community:
“We were doing proofs by transformation versus just proof by axioms, by axiomatic method. And I got some helpful ideas [from the community] about, in the classroom, having my students look at some proofs and approaching them through proof by trans- formation, when we had done it in another way previously.”
Some members described changes in their practice due to their increased awareness of how to teach the course for future educators. These members said that participating in the community helped them to develop a broader perspective on GeT courses, especially in terms of prioritizing the learning needs of pre-service teachers. One commented:
“I would say broadly, the thing that I’ve thought more deeply about is thinking about the teacher side of things as opposed to the math side of things. I’m trained as a mathematician, not a math educator, and so when I’m teaching that course or any of my math courses, I’m thinking to myself as a mathematician. Being in the GeT community, especially where I encounter more math educators, it’s made me more aware that I’m training future teachers when I’m teaching my math courses, and paying attention to those issues.”
In summary, GeT: A Pencil is a community with a goal of supporting members in their efforts to teach GeT courses. Evidence from the evaluation showed numerous examples of how members have connected amidst an ongoing pandemic. Specifically, the evaluation found evidence of members’ willingness to engage with each other in meaningful discussions about teaching GeT. This evidence shows ways in which GeT: A Pencil is accomplishing its goal of supporting members.
References
Borgatti, S. P., & Ofem, B. (2010). Social network theory and analysis. Social Network Theory and Educational Change, 17–29.
Portes, A. (1998). Social capital: Its origins and applications in modern sociology. Annual Review of Sociology, 24(1), 1–24.
Suggested Citation
Gadd, K. (2021, May). Social Networks within GeT: A Pencil. GeT: The News!, 2(3). https://www.gripumich.org/v2-i3-s2021/#social-networks-within-get-a-pencil

Get to know the community
Four questions with Laura Pyzdrowski, Professor of Mathematics, West Virginia University.
- Q1? What is special about your GeT course? In 2-3 sentences, describe your GeT course.
The GeT course that I instruct only has students enrolled who are interested in teaching mathematics. That provides the opportunity to customize the course and focus the curriculum and instruction with that in mind.
- Q2? Who are your students?
My students are primarily undergraduate mathematics majors who have an Area of Emphasis in Mathematics Education (pre-service teachers seeking grades 5 – 12 certification in mathematics). In the future, some students could also be from other majors earning a minor in Mathematics Education via the Mathematics Department.

- Q3? What are you most interested in learning/achieving through participating with the GeT: A Pencil community?
I am engaged in this community so that I can grow professionally and possibly help others who are engaged in that same process. My primary goal is to provide an up-to-date and current GeT course at WVU for pre-service teachers.
- Q4? What is your favorite book you have read in the last few years?
It is difficult to find time to read for pleasure. My husband and I listen to audiobooks when we travel to visit relatives. We are listening to books from the Oregon Trail series by Clive Cussler.
Did you get promoted? Win a grant? Have a baby? Buy a house? We would love to feature your news, whether professional or personal! Email us at GRIP@umich.edu.

Transformation Working Group Update
by Julia St. Goar
In the spring of 2021, the transformation working group created a lesson in the context of transformation geometry, taught and observed the lesson in a group members’ online course, and reflected on the implementation of the lesson. This effort resulted in a publication in the AMS Blogs (Boyce et. al., 2021). The lesson created by the group reflected a variety of content goals including that it should contribute to student understanding of mathematical definition, emphasize mathematical precision, and help develop a culture of sense-making, exploration, and justification.. A further goal was to create an introductory-level, inquiry-based learning lesson that could be easily adapted to be placed into a variety of different types of GeT courses and contribute to student understanding of transformation geometry. The lesson used Adinkra, which are symbols created in Ghana, from the resource created by Eglash et. al. (n.d.).
Moving forward, the group will likely teach different versions of the above lesson in the GeT courses taught by transformation group members, reflect on how it went as a group, and modify the lesson accordingly. More broadly, the group will continue focusing on collecting and creating activities that support student understanding of foundational topics in transformation geometry.
Parallel to the above goals the group has an ongoing goal of formulating an axiomatic system such that (a) its statements are accessible to both college geometry students and high school students and (b) the axioms lead to an efficient system of lemmas and propositions that can be used to deduce major congruence and similarity results. However, instead of formulating the system from scratch, the group is currently exploring various existing axiomatic systems and definitions in transformation geometry (e.g., Douglas & Picciotto, 2017; Venema, 2006) and discussing their appropriateness and applications in the diversity of GeT courses currently represented in the transformation group.
References
Boyce, S., Ion, M., Lai, Y., McLeod, K., Pyzdrowski, L., Sears, R., & St. Goar, J. (2021, May 6). Best-Laid Co-Plans for a Lesson on Creating a Mathematical Definition. AMS Blogs: On Teaching and Learning Mathematics. https://blogs.ams.org/matheducation/2021/05/06/best-laid-co-plans-for-a-lesson-on-creating-a-mathematical-definition/
Douglas, L. & Picciotto, H. (August, 2017). Transformational proof in high school geometry: A guide for teachers and curriculum developers. Retrieved from https://www.mathedpage.org/transformations/proof/transformational-proof.pdf.
Eglash, R., Bennet, A., Krishnamoorthy, M., Sawyer, S., & Adali, S. (n.d.) Adinkra Background. Culturally Situated Design Tools. https://csdt.org/culture/adinkra/index.html
Venema, G. A. (2006). Foundations of geometry. Pearson.
Suggested Citation
St. Goar, J. (2021, May). Transformation Working Group Update. GeT: The News!, (2)3. https://www.gripumich.org/v2-i3-s2021/#transformation-working-group-update

Teaching GeT Working Group Update
by Nat Miller
The Teaching GeT working group continues to work on narratives to accompany the SLOs that we developed and at the same time is incorporating some changes into the SLOs.
The SLOs deal with 10 broad categories:
- Proofs Derive and explain geometric arguments and proofs in written and oral form.
- Proof Verification Decide whether or not geometric arguments given by others are correct.
- Secondary Geometry Understanding Understand the ideas underlying the typical secondary geometry curriculum well enough to explain them to students and use them to inform teaching practice and pedagogy.
- Axioms, Theorems, and Models Understand and explain the relationship between axioms, theorems, and geometric models in which they hold (such as the plane, the sphere, the hyperbolic plane, etc.).
- Definitions Understand the role of definitions in mathematical discourse.
- Technologies Effectively use technologies such as dynamic geometry software to explore geometry.
- Euclid’s Elements Demonstrate knowledge of Euclidean Geometry, including the history and basics of Euclid’s Elements, and its influence on math as a discipline.
- Straightedge and Compass Constructions Be able to perform basic Euclidean straightedge and compass constructions and be able to provide justification for why the procedure is correct.
- non-Euclidean Geometries Compare Euclidean geometry to other geometries such as hyperbolic or spherical geometry.
- NCTM Standards Apply the following NCTM Geometry Standards: (a) analyze characteristics and properties of two- and three-dimensional geometric shapes and develop mathematical arguments about geometric relationships; (b) apply transformations and use symmetry to analyze mathematical situations; and (c) use visualization, spatial reasoning, and geometric modeling to solve problems.
In addition to the SLOs, we included a statement that in addition to teaching these content standards, all Geometry courses for future teachers should give students many chances to experience and develop their abilities with the mathematical process skills of problem solving, reasoning and proof writing, oral and written communication of mathematical ideas, and productive collaboration within groups. They should also get a chance to engage with the progression of exploration followed by making conjectures and trying to prove their conjectures.
So far, the working group has written narratives for SLOs 3, 4, 5, and 9. Several of these narratives are included elsewhere in this newsletter. We are continuing to work on narratives for the other SLOs, with different subgroups spearheading our efforts for each remaining SLO. We will continue to meet Thursdays at 10 AM Eastern every other week throughout the summer and would welcome others to join us.
Suggested Citation
Miller, N. (2021, May). Teaching GeT Working Group Update. GeT: The News!, (2)3. https://www.gripumich.org/v2-i3-s2021/#teaching-get-working-group-update

Upcoming Event
GeT: A Pencil End of Academic Year Community Meeting
Friday, June 11 2PM ET

To submit a paper to be highlighted in a future newsletter, please fill out this form.
GeT Support
Sponsored by NSF DUE-1725837. All opinions are those of the authors and do not necessarily represent the views of the National Science Foundation or the University of Michigan.
Patricio Herbst, PI
Amanda Milewski, Co-PI
Get Support is housed in the GRIP Lab at the University of Michigan
Inese Berzina Pitcher, Project Manager
