
Table of Contents
- Towards the Development of a Prospectus for a GeT: A Pencil Book by Amanda Brown
- Does Our MKT-G Instrument Measure the Same Knowledge in the Same Way for GeT Students and for Practicing Teachers? by Inah Ko, Mike Ion, and Pat Herbst
- What Can We Learn From an Assessment Item About Constructing Perpendicular Bisectors? by Michael Weiss
- On Mathematical Knowledge for Teaching Geometry and the SLOs: A Reflection by P. Herbst
- Transformation of AC2inG Classroom-Based Research Due to COVID-19 by Erin E. Krupa
- Teaching GeT Working Group Update by Nathaniel Miller
- GeT Course Student Learning Outcome #2 by Teaching GeT Working Group Members
- Transformations Working Group Update by Julia St. Goar
- GeT to Know the Community: Dorin Dumitrascu
- Member News
- Upcoming Events

Towards the Development of a Prospectus for a GeT: A Pencil Book
by Amanda Brown
In this past year, the GeT: A Pencil community has been very productive in terms of the dissemination of scholarship about the collaborative work happening within the community. For example, at the time of this writing the GeT Transformations Working Group has shared their work developing and co-teaching a series of lessons focused on the geometric transformations embedded in the Adinkra Symbols in a few outlets—including the 2022 RUME conference (https://www.gripumich.org/2022/04/24/get-a-pencil-represented-at-rume-2022/), the AMTE 2022 conference, and the AMS blog (https://blogs.ams.org/matheducation/2021/05/06/best-laid-co-plans-for-a-lesson-on-creating-a-mathematical-definition/#more-3605). Similarly, the Teaching GeT Working Group has shared their work focused on developing a set of Student Learning Outcomes (GeT SLOs, hereafter) in a variety of contexts—including numerous articles contributed to GeT: The News! and presentations at the 2022 AMTE and 2020 and 2022 RUME conferences (https://www.gripumich.org/2022/04/24/get-a-pencil-represented-at-rume-2022/). Also, several instructors have collaborated with members of the GRIP lab in efforts to share about the formation and development of the GeT: A Pencil community in higher education outlets—such as a chapter for the upcoming Handbook of STEM Faculty Development and a roundtable discussion at AERA (https://www.gripumich.org/2022/04/27/grip-at-the-2022-aera-annual-meeting/).
In light of these efforts, the GRIP Lab recently (January 2022) proposed the idea of advancing the community’s dissemination efforts with the publication of an edited book. Our initial suggestion to the community has been met with enthusiasm, both during the meeting and in the intervening time since that initial discussion. Pat and I have invited Dr. Nathaniel Miller and Dr. Laura Pyzdrowski to join us for some initial discussions regarding how we can get going with the project.
I would like to take this opportunity to report about those conversations and, in doing so, share some of our initial ideas. So far, our meetings have focused on the following topics: (1) what the content of such a book might be, (2) some potential publishers we might approach with the idea, and (3) a rough timeline for ensuring the project is completed in a reasonable timeframe. In what follows, I share details about the first item—our initial ideas about the content of the book—in hopes that you, as part of the community of individuals that read GeT: The News!, will provide feedback we can use to further shape our efforts to envisage what such a book might look like. We conceive of the book being comprised of contributions that fit roughly within six topics that I describe briefly below.
Topic 1: Background about formation of GeT: A Pencil
This topic emerged out of our collective sense that it might be important to provide the reader with some context about the formation of the community. Some of the contributions that might fit within this first topic include: the complexity of the system of improvement that surrounds GeT courses from the perspective of multiple stakeholders; things we have learned about the existing variations in GeT courses from various instruments such as the MKT-G, syllabi collection, instructional logs, and end of course surveys; the ways that an online inter-institutional community can serve as a kind of “virtual mathematics department” focused on development of a course and instruction within a given course; and a retrospective description of the development of GeT: A Pencil. These contributions may help identify the value of the projects the community has undertaken.
Topic 2: Background and elaborations of the SLOs
Contributions to this topic would complement, without simply duplicating, the work that has been ongoing over the last two plus years to articulate the SLOs. Unlike the future SLO website which will contain the “official” elaborations produced by the collective teaching GeT group, we envision the inclusion of this topic as providing opportunities for smaller teams of authors to provide more personal accounts regarding what a particular SLO means to them. In seeking contributions to this topic, we plan to encourage contributors to work in smaller groups in order to produce chapters about some of the diverging perspectives that have emerged during the development of and/or conversations about the SLOs—with the real possibility that there will be more than one chapter per SLO. Our hope is this will result in a focus area that encourages readers to engage with the larger conversations underlying the development of the SLOs by putting these multiple perspectives about the SLOs in conversation with one another. Unlike the SLOs and their elaborations, which speak with a collective voice and articulate a compromise arrived at by a certain date, we surmise that a diverse set of perspectives on the SLOs will help keep alive the various strands of discussion toward the goal of the SLOs being a living document.
Topic 3: Supporting the SLOs in instruction
We hope that the inclusion of this topic would create an outlet for the plethora of efforts within the GeT: A Pencil community and possibly elsewhere to share instructional activities. For example, the inclusion of this topic area could create opportunities for individual or teams of authors to further develop some of the past GeT: The News! articles that have focused on the sharing of instructional activities. Also, this could create an outlet for some of the work on the Adinkra Lesson that has been ongoing in the Transformations Working Group or for expansion on the work that started back at the beginning of our community’s existence in the GeT task repository working group. Crucially, chapters contributing to this topic area will provide the authors with the opportunity to go beyond simply describing an activity, providing space to allow them to account for the activity in terms of how it can help serve in the instructional support of the SLOs. We imagine that both members and nonmembers might want to participate in writing these illustrations and that the editing process could help connect the writing to the SLOs, so that even if someone does not quite know how the activity they do can be connected to any SLO, the printed result will make that clearer. We think this can be a strategy for disseminating the SLOs as well as inviting commitment to the SLOs by others (in this case, authors that publish their activities).
Topic 4: Assessing the SLOs
For this topic area, we seek to include chapters focused on the assessment of the SLOs. This could include contributions focused on the process of constructing items for assessing the SLOs, what we might learn about students or GeT courses from the administration of such items, the uses of such items for various purposes within GeT courses (diagnostic, formative, summative), the construction of different types of rubrics for grading or scores those items (holistic, analytic), and various perspectives on such items and their use with GeT students. We have seen some examples of what this can be like in notes written by Michael Weiss in this and the previous issue of GeT: The News! Again, both members and nonmembers could share assessment activities they use and comment on how these target the SLOs.
Topic 5: Sustaining the work around the SLOs
We thought it might be important to include a topic that looks to the horizons of this work–naming work that is ahead and fleshing out what that might look like. As of right now, this is the least developed topic area, but we are open to ideas. We have some ideas about general terrain that could be named. We also have a few ideas for chapters related to the longer run implications of the SLOs on things like the MKT-G instrument. To be clear, as a group, we are not yet sure if this is its own topic area or something that could be subsumed into the next topic area, as a kind of commentary about the SLOs. But we thought in this early stage, we would at least share the idea about the topic and invite you to respond with ideas you might have in mind. Since the beginning of the community, we have regularly heard from many of you about ideas you have for the ways this work might be expanded and sustained in the years to come. Perhaps this topic area could be a place to start filling out those visions into fuller proposals. Let us know what you think.
Topic 6: Reactions from the Stakeholder communities
For this topic, it might be valuable to have reactions about the SLO work (or perhaps particular chapters from the edited collection) from those that might well represent the stakeholders of the system that contains the problem of improving the capacity for teaching high school geometry. This system includes not only the GeT course but also the institutions that make demands on and provide resources for the course as well as those institutions which stand to benefit from and feed the GeT course. In this topic area, we envisioned inviting contributions the following types of individuals: mathematicians that influence or have, in the past, influenced the GeT course; mathematics educators that have had some investment in the teaching and learning of K-16 geometry; authors of frequently used GeT textbooks; mathematics education researchers who have done basic research on children’s thinking about geometry; mathematicians or mathematics educators with a more international focus on geometry; individuals that have served in administrative roles in university mathematics departments; individuals who have stewarded teacher education credentialing processes at the university; individuals who have played a role in projects that look at improvement in ways different from the strictly institutional perspective; practitioners who have experience working in and with high school mathematics departments to improve geometry instruction; educational researchers who have methodological expertises in the areas of survey and assessment design; and possibly also recent graduates from teacher preparation programs who may have the ambition to write and could bring a fresh perspective.
In sharing these roughly sketched abstracts for the topics to be included in the book, our hope is that in the next month or so you will find ways to reach out to one or all of the four of us and provide your thoughts. This could include suggesting additional topic areas and ways to expand or collapse these topics, along with any other thoughts you might have. So, please, don’t be a stranger. We really do endeavor for this to be a product that serves our collective aims to disseminate about the work we have all been engaged in these last few years together. You can reach us at the following addresses: Amanda Brown (amilewsk@umich.edu), Pat Herbst (pgherbst@umich.edu), Nat Miller (nathaniel.miller@unco.edu), and Laura Pzydrowski (laura@pyzdrowski.ws). We are also planning to have a discussion about this project during the GeT: A Pencil Community meeting on Friday, June 10, 2022 @ 2:00 to 3:30 pm. We are hoping by scheduling it for the same time slot as our seminar series, we will enable as many community members as possible to attend and share their thoughts.
Suggested Citation
Brown, A. (2022, May). Towards the Development of a Prospectus for a GeT: A Pencil Book. GeT: The News!, 3(3). https://www.gripumich.org/v3-i3-sp2022/#towards-the-development-of-a-prospectus-for-a-get-a-pencil-book

Does our MKT-G Instrument Measure the Same Knowledge in the Same Way for GeT Students and for Practicing Teachers?
by Inah Ko, Mike Ion, and Pat Herbst
In order to understand the impact of a teaching intervention (e.g., a course or a professional development program) on what students gained from that experience, students are often administered a test before and after that intervention, and researchers study the gains computed by subtracting the pre-test scores from the post-test. Similarly, researchers use the difference in groups’ test scores to compare performance between different groups. This way of using a difference in test scores, however, requires an assumption that test items measure the same construct (e.g, knowledge) in the same way for different points in time (e.g., pre- and post-test) or different groups of participants (e.g., pre-service and practicing teachers).
To ensure this assumption of measurement invariance (i.e., the same test items measure the same construct in the same way) is important when comparing amounts of, or gains on, a construct, because the observed difference in the scores could be due to different types of constructs being measured by the same items rather than the difference in the same target construct. For example, different groups of participants could interpret the same wording differently due to their demographics or educational background. Similarly, participants could react differently to the same content of an item depending on when the item is provided to the participants. As such, we cannot take for granted that the use of the same assessment items guarantees that a set of assessment items is measuring the same thing across different groups of participants or over time. To validly compare a measured construct across groups or time points, it is recommended that a test of measurement invariance be performed. In other words, it is important to demonstrate that the way in which items are related to a target construct (e.g., MKT-G) is equivalent across the compared populations and over time. The statistical technique used to test this invariance in our study is called multi-group confirmatory factor analysis (Brown, 2006). In this note, we present how we used the measurement invariance tests to estimate the gain of GeT students’ mathematical knowledge for teaching geometry (MKT-G) before and after taking GeT courses and how their post-test score is different from practicing teachers’ MKT-G.
By using the 17 MKT-G items developed by Herbst’s research group, we examined the participating GeT students’ MKT-G growth over the duration of the course. Also, by scaling the growth using a distribution of practicing teachers’ MKT-G scores, we approximated GeT students’ growth in terms of in-service teachers’ years of experience. An assumption in estimating a construct (here, MKT-G) by using a set of responses is that the common variance among a set of responses to items is accounted for by the construct, and the relationship between the scale of an item score and the latent construct is a linear function. The slope of the linear function, where its horizontal axis represents the level of the latent construct and the vertical axis represents item score, is the item factor loading representing the magnitude of the relationship between the item and MKT-G. The intercept of the linear function is a predicted value of the item score when the level of MKT-G is zero. Thus, the equivalence in the way in which items are related to a targeted construct between the groups can be examined by testing the equality in the structure of the construct (configural invariance), factor loadings (metric invariance), and the item intercepts (scalar invariance). We tested the equivalence of item parameters simultaneously, not only between GeT students and practicing teachers but also between GeT students’ pre-test and their post-test.
The results derived from subsequent invariance tests suggested that the relationship of the items to the measured knowledge was at least partially equivalent between GeT students’ pre- and post-test, as well as between GeT students’ and practicing teachers. Here, partial equivalence means that we were able to establish the equivalence between the groups and time points after allowing unequal item parameters (item factor loadings or item intercepts) for 9 among 17 items. As we were able to establish comparable scales, we proceeded to calculate the GeT students’ MKT-G growth and compare the growth to the practicing teachers’ MKT-G.
The comparison of the scores suggested that, on average, GeT students scored about 0.25 SD units higher on the MKT-G test after completing the GeT course, but it was still 1.04 SD units below practicing teachers’ MKT-G who took the same test. This result implies the positive association between the college geometry courses designed for future teachers and mathematical knowledge for teaching geometry in terms of the growth in the knowledge of the students who took the courses. Additionally, examining the association contributes to research methodology by showing how to establish comparable scales of knowledge gains between two different teacher populations (e.g., pre-service teachers and in-service teachers).
Reference
Brown, T. A. (2006). Confirmatory factor analysis for applied research. Guilford.
Suggested Citation
Ko, I., Ion M., and Herbst P. (2022, May). Does our MKT-G instrument measure the same knowledge in the same way for GeT students and for practicing teachers? GeT: The News!, 3(3). https://www.gripumich.org/v3-i3-sp2022/#does-our-mkt-g-instrument-measure-the-same-knowledge-in-the-same-way-for-get-students-and-for-practicing-teachers

What Can We Learn From an Assessment Item About Constructing Perpendicular Bisectors?
Part 3: Looking at student responses and expert anticipations of those responses
by Michael Weiss
University of Michigan, Department of Mathematics
Introduction
This is the final installment of a three-part deep dive into a single assessment item the GRIP team designed to probe students’ knowledge of the student learning objectives (SLOs). Item 15301 was written for the purpose of investigating SLO 3, Secondary Geometry Understanding: Understand the ideas underlying the typical secondary geometry curriculum well enough to explain them to their own students and use them to inform their own teaching. The item asks:
Mr. Gómez taught students the usual procedure for constructing a perpendicular bisector for a segment. Veronica asked Mr. Gómez to explain why the construction works, meaning how they can be sure that the line that is constructed is indeed perpendicular to the segment and passes through the midpoint. How could Mr. Gómez explain that?
In the first two parts of this deep dive, I discussed this item from an a priori perspective. I observed that this item actually consists of multiple nested questions. First, there is the question posed to Mr. Gómez by Veronica within the situation of teaching; I refer to this as the “internal question.” Second, there is the question posed to the GeT students themselves about the situation of teaching; I call this the “external question.” In addition to these two questions, I also discussed various “foundational questions” about the mathematics of geometric constructions.
In what follows, I briefly summarize some of the main ideas of that a priori analysis and use those main ideas to propose a collection of codes for themes that we might expect to find represented in students’ responses to item 15301. These codes will then be used to examine two sources of data: first, a collection of responses to item 15301 produced by a cohort of 47 GeT students; and second, a collection of comments on item 15301 from a group of experienced GeT instructors who participated in a workshop in Summer 2021. These data sources will allow us to explore the following questions:
- What themes are represented in students’ responses to item 15301?
- What themes did the GeT instructors anticipate would or could be present in students’ responses?
- What did GeT instructors notice when they were given the opportunity to examine students’ responses directly?
We begin with a very brief review of some of the ideas developed in the first two parts of this analysis. In the first part, I sought to problematize the foundational question “Can we construct a perpendicular bisector?” as follows:
- First, I observed that the answer to the questions “Can we construct a given geometric object, and, if so, how?” depends, in a highly nontrivial way, on what axiomatization we use for our geometry. For example, in a “compass and straightedge” geometry (as in Euclid’s Elements), angle trisectors cannot be constructed at all; however, in more modern “ruler and protractor” geometries, their construction is trivial. Even for the case of the construction of a perpendicular bisector, which is possible in both systems, the question of how to enact such a construction differs significantly between the two systems.
- Second, from a rather literal point of view, no geometric construction ever perfectly produces its intended object. Any construction inevitably falls short because of two categories of limitations: (a) user error, such as an unsteady hand, a ruler that slips on the page while a line is being drawn, etc.; and (b) intrinsic limitations owing to the fact that the “points” and “lines” we draw (and draw on) are not really points and lines but merely symbolic representations of them. For this reason, the physical marks drawn on actual paper (or in a digital representation) are never more than approximations of the conceptual objects they represent.
- This last observation, regarding the mismatch between idealized geometric objects and actual drawings, cuts both ways—just as no actual construction in the real world can perfectly produce the object it is intended to generate, it is also the case that even a mathematically “incorrect” construction algorithm may, in some cases, produce a result that is close enough to be indistinguishable from what is sought.
Veronica’s question is thus more problematic than it seems at first. In seeking to understand why a given construction is valid, she (potentially) raises deep questions about the structure of our geometric knowledge, its contingency on certain conventions of definition and axiomatization, and the relationship between the ideal world of mathematical abstraction and the real world of experience and measurement.
Following this discussion, we turned to a close reading of item 15301 and noted that Veronica’s question (the “internal question”) is actually formulated in two not-quite-identical ways. It is first formulated as a request for an explanation of “why the construction works”, the item immediately reframes this as “How can we be sure that the line… is indeed perpendicular to the segment and passes through the midpoint?” Whereas the first question calls for an explanation, the second seeks a verification. Corresponding to these two questions, students might respond in one of two ways:
- Students might provide a mathematical argument for why the construction is a valid one, or
- Students might appeal to empiricism as a means of verifying that the product of the construction algorithm has the intended properties.
These two broad themes may be further subdivided into sub-themes. A mathematical argument may make use of synthetic methods (as, for example, in a traditional two-column proof), analytic methods (as in an argument that uses coordinate geometry to transform the geometric question into an algebraic one), or transformational approaches. Any of these approaches could be presented as either a formal proof or a less detailed argument that indicates the main points of what could go in a formal proof.
Likewise, an empirical approach to answering Veronica’s question could take different approaches, depending on whether the student perceives the underlying problem as a concern for user error or feels a degree of skepticism regarding the reliability of the method itself. In the former case, a response might emphasize the need to exercise caution when using the construction tools. In the latter case, a response might suggest using measurement tools to verify the result of the construction after the fact.
Finally, in our discussion of the external question (“How could Mr. Gómez explain that?”), we observed that a GeT student’s anticipation of Mr. Gómez’s response could draw on multiple domains of knowledge within the construct of Mathematical Knowledge for Teaching (Ball, Thames, & Phelps, 2008). Such a response might call upon Knowledge of Content and Curriculum (KCC), Knowledge of Content and Students (KCS), Knowledge of Content and Teaching (KCT), and Horizon Content Knowledge (HCT).
Thus, when we turn to the responses of the cohort of GeT students and instructors, we expect that we may find some or all of the following themes present:
- A theory-building disposition (Weiss & Herbst, 2015) —a sensitivity to the particular axiomatic structure in use for one’s theory of geometry, and an awareness that it is only one of many possibilities;
- A tendency towards skepticism—an awareness that constructions presuppose flawless operation with idealized tools that cannot be executed in the real world;
- An orientation towards pragmatism—a willingness to accept an imperfect construction as long as the result is close enough to the desired one;
- A mathematical argument, which may take the form of either a formal proof or an informal argument;
- An empirical disposition, which may take one of two forms:
- exercising caution in the use of tools and execution of the algorithm, or
- the use of measurement tools to verify the accuracy of the completed result;
- One or more knowledge domains within MKT.
In the next section, we describe the data sets in more detail and use the themes above to classify the responses of our students and instructors.
Data sources and methods
Assessment item 15301 was pilot tested in Spring 2021 with a cohort of 47 GeT students associated with six different instructors and/or universities. Seven of those students provided no response to the item; another eight responded with “I don’t know,” “Unsure,” or similar responses. The present analysis is based on the responses of the remaining 32 students. The item was included in an assessment conducted online using a Qualtrics survey. Because the assessment platform only allowed responses in the form of typed text, many modes of communication that might otherwise have been called for (including not only diagrams but also mathematical notation) were not available to respondents. For this reason, it seems prudent to be somewhat skeptical of the data; it is likely that students’ responses may have been quite different (and, one suspects, richer) had the assessment been administered in a paper-and-pencil format.
After the assessments were administered, a group of six college-level Geometry instructors with varying levels of teaching experience came together in Summer 2021 for a virtual workshop organized around examining students’ responses to the assessment items. Among these instructors were both mathematicians and mathematics educators; most of them had taught a course specifically targeted at Geometry for Teachers (GeT), although at least one taught a Geometry course that was not explicitly “for teachers.” In each meeting of the workshop, participants were asked a series of questions about four assessment items. Participants were asked to describe not only what they would consider to be a good response to the item but also what they expected a student might say in response. Participants were then shown the set of student responses and asked to describe what they saw in those responses.
In analyzing the two sets of responses, I used the following methodology. First, each student response was tagged with one or more of the following codes: THEORY-BUILDING, SKEPTICISM, PRAGMATISM, ARGUMENT, CAUTION-TOOLS, MEASUREMENT, and MKT. These seven codes correspond to the themes enumerated at the end of the previous section. A response would be coded with a given tag if it could be construed as invoking or alluding to the corresponding theme. Thus, for example, the tag ARGUMENT was used for any response that seemed to be suggesting or calling for a formal proof, whether or not such a proof was actually provided. The same codes were then used to tag GeT instructors’ responses. In principle, a single item could be tagged with more than one code; in practice, none of the items were found to contain evidence of more than one of the themes.
Student responses to Item 15301
Of the 32 responses from GeT students, eight were not tagged with any of the codes above. Most of these amounted to nothing more than a restatement of the property in question: for example, “By showing the slopes are perpendicular and that the two segments are equal,” “Show that it creates a 90 degree angle,” and “A perpendicular line creates a 90 degree angle.” Such responses do not explain, or even hint at, how one would show those properties. Another response consisted simply of the two words “the center.” It is impossible to know what the respondent intended by this or if it was the result of an error in entering their response. The longest untagged response read:
The circles we create help us visualize. Consider that these two circles would overlap. We can assume that inside this overlap is where the midpoint is. By constructing the perpendicular bisector in this manner, this is the best way to ensure that it is consistent.The circles we create help us visualize. Consider that these two circles would overlap. We can assume that inside this overlap is where the midpoint is. By constructing the perpendicular bisector in this manner, this is the best way to ensure that it is consistent. (Response A53)
Although this student had quite a lot to say, I was unable to interpret exactly what was intended by this response.
Of the remaining 24 items, 16 responses were tagged with the code ARGUMENT. None of these responses were fully-developed mathematical proofs, but some of these responses sketched out an argument that could be plausibly interpreted as the outline of one. For example, one response (A19) read, “He could use the perpendicular bisector theorem.” Although lacking in details, this does indicate an efficient method for proving that the construction is valid. Another student responded:
Show how the two circles have the same radius meaning the intersections are the same distance away from each point and there are two points of intersection which are necessary for the creation of a line. (Response A29)
The argument here is not fully coherent, but it does seem clear that the student was at least attempting to provide some sort of mathematical argument or informal proof. Most responses tagged with the code ARGUMENT were of this sort. Although they did not contain a fully correct or convincing mathematical argument, they contained evidence that the student at least understood the question to be calling for one.
However, not all students understood the question as calling for a mathematical argument. Six responses indicated that the student understood the question as calling for some kind of empirical measurement, rather than a theoretical justification. Typical responses tagged with the MEASUREMENT code were:
- “Measure the segment before bisecting it and then measure it after bisecting” (A55)
- “Measure the angles around the intersection. If one of them is 90 degrees, then it is perpendicular. Then measure each side of the segment, and if they are equal then it is a perpendicular bisector.” (A51)
- “Use a compass and a ruler to measure.” (A32)
In addition to these, two responses were tagged with the CAUTION-TOOLS code:
- “Making sure you accurately use your geometric construction tools and are precisely lining up to each point.” (A5)
- “With the use of a straightedge it can be sure to be perpendicular” (A26)
These three codes — ARGUMENT, MEASUREMENT, and CAUTION-TOOLS — were, in fact, the only three codes used. Thus, at a very coarse level of description, we can say that about half of the responses indicated that the student understood the question as calling for a mathematical argument of some sort; a quarter of the responses indicated that the student interpreted the question as calling for some kind of appeal to empiricism; and the remaining quarter contained either no meaningful content or none that could be classified. None of the student responses gave any indication that students were thinking about any of the foundational questions discussed in Part 1 of this essay or drawing directly on any of the specialized content knowledge domains discussed in Part 2.
Instructor responses to Item 15301
- What do instructors think is necessary knowledge for Item 15301?
In the summer workshop, the six instructors were initially asked the question “What is the knowledge needed to answer this item?” All six instructors either provided a mathematical proof or discussed what prior knowledge one would need in order to provide a mathematical proof; every instructor interpreted the item as calling for a mathematical argument. Examples of these responses are:
- “The construction forms a rhombus and the diagonals of a rhombus are perpendicular and bisect each other. A point equidistant from the endpoints of a segment is on the perpendicular bisector of the segment.”
- “Reflexive property (segments), then SSS, then CPCTC, then SAS, then linear pair of angles.”
- “Knowing that the diagonals of a rhombus are perpendicular and bisect each other gives the result immediately (I’ll note that in my years of teaching constructions, few GeT students remember this since we haven’t discussed it in class). More often, they take an approach like the one [other instructor] mentions: using two triangle congruences to show constructed line is perpendicular to AB and that it bisects AB. So the argument requires experience/understanding of triangle congruence proofs.”
As the three examples above show, responses varied significantly in how much detail was provided and how many alternatives the workshop participants entertained. However, each of these responses understands the prompt as an invitation to provide a mathematical proof or, at least, the outline of one.
Two instructors included in their responses some reference to the fact that what counts as a proof may vary depending on the type of geometry being taught (synthetic, analytic or transformation-based). One such response, for example, included the following:
The most efficient way to solve this problem is to know that a point is on the perpendicular bisector of AB if and only if it is equidistant from A and B. One either needs to quote the result, or to prove it… A transformation-based approach could work as well: the initial figure, AB, and the construction protocol, are both invariant under the act of reflection across the perpendicular bisector of AB, and therefore the line constructed must be as well. Therefore the line constructed is the perpendicular bisector of AB.
None of the instructors made explicit reference to the situated aspect of the item prompt; they did not refer to the fact that Mr. Gómez’s response was to be addressed to a student in a high school classroom. We could imagine, for example, responses that referred to ways of knowing or misconceptions that are common among secondary students or that discussed the fact that what would work as an appropriate answer might depend on the curriculum being taught, etc. The fact that none of the GeT instructors, when asked “What knowledge is needed to answer this item?”, responded “They need to know something about how students learn proofs” or “They need to know that proving constructions is not common in many secondary curricula” suggests that they approached this problem primarily as a mathematical task, not as a task of teaching. In terms of the a priori analysis in the first part of this paper, we could say that they discussed the knowledge needed to answer the internal question but not the knowledge needed to answer the external question.
- How do instructors expect GeT students to respond to item 15301?
Workshop participants were next asked to anticipate what type of responses they would receive from GeT students. Only four of the instructors responded to this question, but all four of them expressed an anticipation that students would provide a mathematical argument of some sort. The four responses were:
- “The arcs intersect at two points that are equidistant from the endpoints of the segment (by construction). Therefore, when a line is drawn using those two points, a perpendicular bisector is formed.”
- “One student might reference parallel lines followed with a rotation of 90 degrees from the midpoint makes perpendicular lines. To explain perpendicular bisectors. Another student might use the the curvature in the first quadrant in relation to the intersecting lines to find 90 degrees. Then conclude the intersecting lines are perpendicular. Another student may not want to use the curvature of the lines and reason with triangles.”
- “I would guess that a few people might come up with a correct deductive proof. More if they were in a course that covered constructions and specifically emphasized the ‘proving why it works’ step of constructions. (It is interesting that this question is premised on a teacher teaching the constructions without that vital last step.) I would expect that many would say something like, ‘you can see this will always happen because they are the same distance away.’ Such an argument might actually have more merit than it would initially appear since it would relate to the symmetries.”
- “I would expect most GeT students would start proving pairs of triangles congruent to each other. Quoting the perpendicular bisector theorem seems unlikely to me, as does recognizing this as a rhombus and citing the property of the diagonals of a rhombus.”
While there are clear differences among these responses, particularly with respect to how much variation in student responses the individual instructors anticipate, they all share an interpretation of the problem as calling for a mathematical proof of some sort. None of the instructors expected that the item would call forth an empirical response from a GeT student nor that it would evoke a discussion of theoretical considerations, secondary students’ conceptions of geometry, variations in curriculum, or any other SCK-related topics.
- What do instructors notice in GeT students’ responses?
At this point in the workshop, instructors were shown the 32 student responses described above and were asked to comment on which ones included evidence that the students did, or did not, have the knowledge needed to respond to the prompt. In the ensuing discussion, one instructor identified just four responses as containing at least some evidence that the student contained sufficient knowledge to answer the question. Another instructor described three responses as being “on the right track.” (It is, perhaps, noteworthy that these two instructors identified only a single student in common.) Yet a third instructor wrote:
It is interesting that no one tried to answer this prompt! None of these are as good as I might hope. I wonder if any of them did justifications of constructions in their courses. It doesn’t look like anyone remembered having done this one. But, at the same time, some of these are not so far off. A19 is correct and is a reasonable answer. (The perpendicular bisector theorem says a point in on a perpendicular bisector of AB if and only if it is equidistant from A and B.) A7 is also close to this idea. A34 is close to an idea of the beginning of the symmetry proof.
Two instructors zeroed in on an empirical conception of mathematical justification as being a significant feature of the GeT students’ responses. One of these instructors wrote, “There are (at least) two really important misconceptions that I see: (1) If it looks correct, then it is correct because we constructed it with straightedge and compass (A5, A25). (2) We can measure it with a ruler or a protractor to see that it’s correct (A15, A17, A55).”
- What other kinds of knowledge do instructors see as potentially embedded in Item 15301?
Finally, instructors were asked to comment on which Student Learning Objectives (SLOs) were potentially involved in answering Item 15301 and to add any additional comments on the item. Instructors identified SLO 8 (“Be able to perform basic Euclidean straightedge and compass constructions and be able to provide justification for why the procedure is correct”), SLO 1 (“Derive and explain geometric arguments and proofs in written and oral form”), SLO 5 (“Understand the role of definitions in mathematical discourse”), SLO3 (“Understand the ideas underlying the typical secondary geometry curriculum well enough to explain them to their own students and use them to inform their own teaching”), and,—at least potentially—SLO 7 (“Demonstrate knowledge of Euclidean Geometry, including the history and basics of Euclid’s Elements, and its influence on math as a discipline”).
Instructors also observed that the item contained two different statements of (ostensibly) the same question:
The statement, ‘why something works’ and ‘how can we be sure it is correct’ are not the same thing. I think most GeT students responded to the second part of the question, not the first part of the question. And I do think that second question connects more to the CCSS-M math standards (i.e. using appropriate tools strategically).
When prompted to consider what other kinds of knowledge instructors see as potentially embedded in the item, some instructors did identify issues related to student thinking and curriculum—issues that, as noted above, were not evoked by the prompt, “What do students need to know in order to answer this question?” For example, two instructors observed that the appeal to empiricism is somewhat unsurprising, given what is common in secondary Geometry classrooms. One wrote:
Perhaps GeT students are trying to imagine themselves in the hypothetical situation of responding to a student who has not yet learned triangle congruence proofs etc. I think this is pretty typical for how constructions are introduced; students are taught the steps as they are learning the definitions for the geometric objects… So the ‘how can we be sure it is correct’ regards what is available to those students at the time: getting empirical evidence using other tools they know how to use that the construction meets the requirements of the definition of perpendicular bisector.
The other wrote:
I also think this question is potentially very revealing of the different proof schemes that GeT students hold, in particular their tendency to default to empiricism in the context of construction problems. Whether we call that a ‘knowledge’ issue is another matter; I would prefer to describe this in terms of ‘different ways of knowing’, rather than ‘correct’ / ‘incorrect’. But we do know that justifying a construction with a proof is (bizarrely) not normal in the classroom, no matter how much we would like it to be.
Discussion
Despite instructors’ rather pessimistic appraisals of the GeT students’ work, it bears repeating that roughly half of all responses indicated that students interpreted the prompt as calling for some kind of mathematical argument. It is true that most of the arguments they offered fell far short of what most GeT instructors would accept as a correct proof; however, we should, perhaps, take some comfort in the evidence that a significant portion of the students have at least been enculturated into mathematical practice and its sensibilities enough that they understand that a question in the form of “How can we be sure that this works?” is supposed to be answered with a proof.
In contrast, it seems significant that none of the instructors anticipated that GeT students would respond to the prompt with an empirical strategy, either one that focuses on controlling the means of production or on one that emphasizes measuring the output of the algorithm. This may indicate a substantial “expert blind spot” for GeT instructors; we are so thoroughly accustomed to approaching mathematics teaching from the perspective of what is mathematically correct that we forget that these cultural norms do not come naturally to students and should not be taken for granted. If we, as GeT instructors, think that a proof-centric approach to mathematical validation is the sine qua non of secondary Geometry instruction, it is vital that we recognize that our future secondary teachers do not automatically share that value and that other forms of validation (such as an appeal to authority or empiricism) need to be not only anticipated but also confronted directly in the GeT classroom.
It also seems significant that issues related to the situated nature of the task—the fact that the external question is not just a mathematical problem but a problem of mathematical teaching—were not mentioned by any of the GeT students nor by any of the GeT instructors in their response to the initial question “What do students need to know in order to answer this question?” This suggests that students and instructors alike may tend to default to the role of mathematical problem-solvers, rather than consider other specialized domains of knowledge that are important for mathematical teaching. It may be worth considering whether those other domains of knowledge—knowledge of how students think about proof, of how different curricula do or do not establish relationships between geometric constructions and axiomatic systems, etc.—could or should play a larger role in the objectives of a Geometry for Teachers course.
References
Ball, D.L., Thames, M.H. & Phelps, G. (2008). Content knowledge for teaching: What makes it special? Journal of Teacher Education 59(5), 389-407.
Weiss, M., & Herbst, P. (2015). The role of theory building in the teaching of secondary geometry. Educational Studies in Mathematics, 89(2), 205-229.
Suggested Citation
Weiss, M. (2022, May). What can we learn from an assessment item about constructing perpendicular bisectors? Part 3: Looking at student responses and expert anticipations of those responses. GeT: The News!, 3(3). https://www.gripumich.org/v3-i3-sp2022/#what-can-we-learn-from-an-assessment-item-about-constructing-perpendicular-bisectors

On mathematical knowledge for teaching geometry and the SLOs: A Reflection
by P. Herbst
I want to use this occasion to reflect a bit on what the development of a consensual list of Student Learning Outcomes (SLOs) represents vis-a-vis the field of mathematics teacher education and, in particular, its curricular history. I want to suggest that GeT: A Pencil has helped the larger mathematics education community make progress in identifying how it is that knowledge from the field of mathematics education (particularly the empirical notion of mathematical knowledge for teaching) can be reconciled with the geometric content that has traditionally been curated by mathematicians for its use in designing the curriculum of geometry courses for teachers.
For a long time, the question of what content should be covered in college geometry courses was one that involved the curricular organization of the mathematical domain of geometry. In this work of curriculum design, the considerations made concerned the history and scope of the subject and the different sequences in which the subject could be presented. In that sense, it was no different than how the content for other mathematics courses (e.g., calculus) might be experimented with. Facing the question of what geometry should be taught to teachers, this approach suggested the need to inquire within the mathematical domain of geometry and find topics and organizations of those topics that arguably would serve to educate future teachers. A premium was put on logical organization, aesthetic or historical value, and ease of understanding—not necessarily on readiness for use in teaching.
As research in mathematics education started to inquire about mathematics teachers’ knowledge, one important insight that emerged was that when teachers engage in the work of teaching, they also do mathematics. Tasks of teaching, such as creating or modifying problems for students or determining the mathematical qualities of work that students do (e.g., consistency, correctness, generality) involve the teacher in doing mathematics while teaching. Appropriately, scholars have called these mathematical tasks of teaching (e.g., Ball et al., 2008). While some of this mathematical work could clearly be filed under topics within the curricular organization of a mathematical domain (e.g., making up problems about isosceles triangles surely draws from knowledge of isosceles triangles that could be covered in geometry courses), other mathematical work teachers do could be described as so specialized to the work of teaching that it might not be common among people who otherwise knew a mathematical domain. For example, understanding why point P in Figure 2, below, cannot possibly be the center of a circle tangent to line a at A is a problem a teacher would need to solve when confronting this proposed solution to a construction problem by a student; yet wrong solutions to problems are rarely part of what one learns in mathematics courses.
This distinct mathematical knowledge for teaching is by no means as explicit as the knowledge documented in textbooks. One sees it manifested in actions (e.g., in teachers’ noticings or decisions), recognized by mathematically educated observers, and organized using resources from empirical research (e.g., typologies). One way in which researchers in mathematics education organized this knowledge–the domains of MKT offered by Ball et al. (2008)–was serviceable in demonstrating the diverse epistemological sources of the mathematical knowledge teachers use. The distinction between specialized content knowledge (SCK) and knowledge of content and students (KCS), for example, highlighted that while some knowledge special to teachers is purely mathematical (i.e., the truth or falsity of this knowledge could be established using mathematics alone; e.g., one can prove that point P can never be the center of a circle tangent to a at A), other knowledge also special to teachers might depend on blending mathematical and empirical knowledge (i.e., the incidence of particular error in a student population; e.g., how often does this idea come up when students are asked to construct a circle tangent to two intersecting lines? How hard is it for students to understand why the “solution” proposed in Figure 2 is incorrect?). This epistemological distinction among domains of mathematical knowledge for teaching has been useful for creating assessment instruments; it has helped create blueprints for the different types of items that need to be developed to tap the construct mathematical knowledge for teaching in all its aspects.
When we started the GeT Support project in 2017, the GRIP team had already invested some effort in the development of an assessment instrument whose items were useful to measure the amount of MKT-G (mathematical knowledge for teaching geometry) a teacher has (Herbst & Kosko, 2014). I note that the instrument measured the amount of MKT-G, taking this as a single construct; the instrument does not verify that the individual knows any concept in particular. This instrument had been used to assess the amount of MKT-G in a national sample of high school mathematics teachers, and part of the idea of the GeT Support project was that the same instrument might be of use to inform instructors and the public about the contribution GeT courses could make to increasing capacity for geometry instruction. In the context of the GeT Support project we have indeed been able to gather data that shows that the same instrument can detect changes in MKT-G students’ experience during the time they take a GeT course (see Ion, 2020 ; Ko, Ion, & Herbst, this issue). The items in that instrument illustrate the construct (MKT-G) in general; each item is situated in the context of a task of teaching geometry and presents a problem that a teacher may need to solve in that context. The items are related to the general theory of MKT (Ball et al., 2008) in that each of them avowedly assesses knowledge of one of four domains of MKT (CCK, SCK, KCS, KCT), and the items sample content from the high school geometry curriculum.
We showed examples of those items at our 2018 conference in Ann Arbor. Yet, not every GeT instructor recognized those items as examples of the knowledge that they taught their students in GeT courses. More importantly, it was clear to all, including ourselves, that the items themselves were not, by themselves, useful to think about the content for GeT courses. A reason for it is that the items are just very small bites of knowledge; they might suggest problems to solve, but they do not clearly point to the larger units in which the knowledge covered in a course gets structured. In that sense, they are hard to relate to the sort of curricular work described in the first paragraph.
As a mathematics teacher myself, one way I think of this different granularity of knowledge is with the knowledge exchange diagram shown in Figure 1. On the one hand, concepts and theorems are relatively large objects of knowledge or mathematical ideas that might be at stake in a course. These objects of knowledge are instantiated in many smaller problems or in particular actions in solving such problems. The work on problems and tasks, on the other hand, makes room over time for a large number of small things–noticings, intentions, ways of seeing, tricks, etc. (e.g., representing b as (ab)/a) that are part of the ways of doing mathematics, part of the mathematical sensibility. Some of the mathematics done in the context of problems and tasks may never receive a name or be taught by itself.
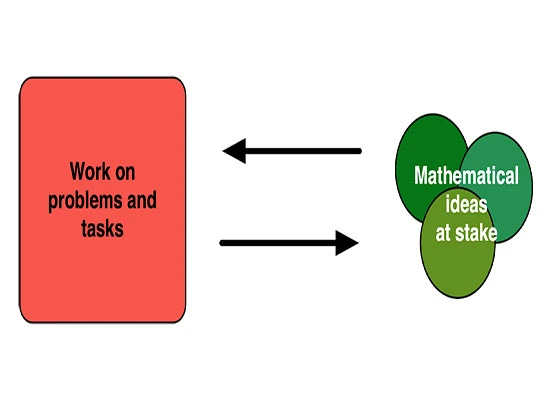
The exchange diagram opens up the possibility to realize that the same object of knowledge can have many different meanings depending on the various problems in which it is operational. For example, the theorem that says that a tangent is perpendicular to the radius of a circle at the point of tangency can be at stake in a number of tasks. It can be useful to come up with a method to construct a circle tangent to a given line; it can also be useful to argue why point P in the diagram below cannot possibly be the center of a circle tangent to line a at point A. In the first case, one uses the theorem to identify the locus of the center of the circle: It must be on the perpendicular to a at A. In the second case one uses it to feed a proof by contradiction: If PA was the radius of the circle tangent to a, then the angle PAO is right and the triangle OPA would be isosceles and with two right angles. The example illustrates how a given object of knowledge has various meanings that emerge in the context of different problems. This is not only the case for the knowledge we teach in mathematics courses, but I surmise it would be reasonably the case for mathematical knowledge for teaching.
The exchange diagram can be useful to explain how the notion of mathematical knowledge for teaching could inform curricular work in GeT courses. Problems like the ones in MKT items are candidate examples for the mathematical work in the red square on the left. Consider, for example, problems like those shown in Figures 3 and 4.
| Mrs. Miyakawa wants to assign a proof problem using the diagram below. If she asks students to assume (i.e., take as given) that ABCD is a rectangle, E is the midpoint of DC , and AE ⏊BE , what could she ask them to prove? | In Mr. Desimone’s geometry class, kites were defined to be quadrilaterals with two distinct pairs of congruent adjacent sides. He then asked his students to draw a kite that has congruent diagonals and two pairs of congruent opposite angles. Andrea came to him in distress after a few minutes saying that she’d tried all sorts of angle measures and diagonal lengths and all she could come up with were squares. Mr. Desimone told his student teacher that Andrea did not understand what the definition of kite means. What do you think Mr. Desimone means by that? |
| Figure 3. Problem 15102 | Figure 4. Problem 15503 |
The two problems in Figures 3 and 4 describe situations in which a geometry teacher might need to do some mathematics while teaching. Using the exchange diagram, they both belong in the red square. But what are the green circles that those problems exchange for? In other words, what is the knowledge at stake in those problems? The mathematical domain of geometry has had expository treatises like Euclid’s Elements, Hilbert’s Grundlagen, or Moise’s Elementary geometry from an advanced standpoint within which one can locate the knowledge at stake in problems, but MKT-G problems have not had similar resources. The difficulty is not that problems like those in Figures 3 and 4 cannot be classified into topics; they could be classified in, perhaps, even more than one topic. But where would they make a difference? Because they can be classified in multiple ways, it is unclear how one would build critical masses of them to serve the creation of problem sets and units of study. Indeed, many such items could be created. How would we know what to emphasize?
With the introduction of the SLO, the picture gets a little clearer. The SLOs have two important virtues that recommend them as candidates to be the green circles in the exchange diagram. First, they have come from a thoughtful process of negotiation and argument among a group of instructors that includes mathematicians and mathematics educators. Second, in arguing for them, both considerations of their stature in the domain of geometry and in the teaching of high school geometry have been made. As a result, if one looked at them only with the eyes of a mathematician or only with the eyes of a teacher educator, these SLOs might appear heterogeneous. I tend to think that is a good thing.
Having arrived at the SLOs and now having elaborations of the SLOs in various issues of this newsletter, our community has an important scaffold for the question of what content could or should be taught in GeT courses. The SLOs can, at a minimum, be a checklist; one could look through problem sets, notes, and syllabi and see where there are topics that match the SLOs. However, the SLOs can also be used generatively and along with other aspects of mathematical knowledge for teaching.
For example, one could see that problem 15503 (Figure 4) can be associated with the role of definitions in mathematics (SLO 5). One could also see that it deals with a mathematical task of teaching, interpreting what students do in response to problems, and that it involves specialized content knowledge about quadrilaterals. In fact, the topic of quadrilaterals might be a good host area to anchor the teaching of SLO 5; Usiskin (2007) wrote a monograph on definition using the classification of quadrilaterals that might support firming up these connections. An interesting issue, perhaps an idiosyncrasy, with quadrilaterals in high school geometry that reveals the value of this topic for the study of the role of definitions is that the HSG curriculum tends not to be consistent in how definitions of special quadrilaterals are read. While rectangles and rhombi are understood as defined inclusively (e.g., squares are rectangles), trapezoids are understood as defined exclusively (e.g., parallelograms are not trapezoids). One possibility afforded by this consideration is that instructors might use a unit on quadrilaterals to aim at the achievement of SLO 5 and, in that context, have their students work on a number of problems in which both quadrilaterals and definitions are addressed in the context of tasks of teaching.
Overall, I believe that the SLOs provide us with a way into creating a curriculum for GeT courses that can bridge the mathematical topics that have been used to organize geometry instruction in the past and the particular occasions in which a teacher might have to do mathematics while teaching geometry. Without downplaying the value of collaboration and consensus in forming a community of colleagues, an important achievement of the SLOs is to have helped us figure out how the idea of mathematical knowledge for teaching can become part of curriculum making.
References
Ball, D. L., Thames, M. H., & Phelps, G. (2008). Content knowledge for teaching: What makes it special?. Journal of Teacher Education, 59(5), 389-407.
Ion, M. (2020). Reporting on the MKT-G results from GeT Students. GeT: The News!, 1(3)
Ko, I., Ion, M., & Herbst, P. (this issue). Does our MKT-G instrument measure the same knowledge in the same way for GeT students and for practicing teachers? GeT: The News! 3(3)
Suggested Citation
Herbst, P. (2022, May). On mathematical knowledge for teaching geometry and the SLOs: A reflection. GeT: The News!, 3(3). https://www.gripumich.org/v3-i3-sp2022/#on-mathematical-knowledge-for-teaching-geometry-and-the-slos-a-reflection

Transformation of AC2inG Classroom-Based Research Due to COVID-19
by Erin E. Krupa
My introduction to the GeT community was attending the Teaching GeT working group a week before I presented a seminar to the group in November of 2020. I wanted to get to know the community before I presented my NSF-sponsored DRK-12 grant (DRL 1907745), Using Animated Contrasting Cases to Improve Procedural and Conceptual Knowledge in Geometry (AC2inG), which had just completed its first 15 months. During that presentation, I set the theoretical framework, grounded in research from cognitive science and extended to mathematics education, for using contrasting cases in learning eighth grade geometry content.
In midst of the pandemic my research team had only been able to work on the curriculum development, so the presentation focused on grounding our curricular design. One thing that makes the AC2inG materials (Krupa et al., 2019) unique is that we created the first web-based contrasting cases in mathematics, and we harness the visual nature of geometry; the cases are animated to highlight key geometric concepts. As we created our materials, we considered several design features: animations and colors to draw student’s attention to the geometric content in meaningful ways, characters’ methods purposefully selected to spark comparisons, geometric thinking of fictitious characters, and diversity of characters throughout the units.
In short, our digital curricular materials place two fictitious students’ voices at the center of mathematics learning, and each lesson includes five unique features: a page for the first fictitious student’s solution strategy on a given geometry task, a page for the second fictitious student’s solution to a geometry task (which could be the same or different task shown on first student’s page), a page with both students’ strategies side-by-side, a discussion sheet with four questions for the students to answer, and a thought bubble page summarizing the key mathematical concepts in the problem. The side-by-side pages are where students really focus on comparing and contrasting the solution strategies. The discussion sheet and thought bubble page are designed to make the instructional goal of each Worked Example Pair (WEP) more explicit and to scaffold discussions among students as they summarize their work from the WEPs (Star et al., 2015).
We were unable to test our interventions in schools in the spring of 2020 and throughout the 2020-2021 school year since schools were closed, and virtual learning stressed the educational system. We had to pivot from our original plan of implementing our digital materials with students in classrooms. It was very tough to let go of the original goal—one that had been conceived meticulously, approved by the NSF, confirmed by external reviews, and vetted by our advisory board. Unable to conduct our randomized-control design, what I needed was student feedback from using the materials. So, we transitioned to conducting virtual think alouds with students across the United States.
Last spring, we conducted 56 hour-long open-ended semi-structured clinical interviews (Piaget, 1976; Opper, 1977) in the form of think alouds with individual participants (n=42). Our goal was to elicit student thinking as participants engaged with the materials and discussion questions, not to get them to a “correct” response (Opper, 1977). In order to engage participants in each phase of the WEP during the interviews, we followed a detailed protocol: examine the first method, examine the second method, horizontally compare the two methods, solve the problems on the discussion page, and read the thought bubble at the end. If needed, we had questions for each phase of the protocol to probe student thinking. In all, there were 3,249 turns that were coded.
Of the 3,249 instances, 1,354 (41.67%) were coded as geometric thinking of the student, 756 (23.27%) were students making comparisons between the WEP characters, 621 (19.11%) were instances of students analyzing the geometric thinking of the WEP characters, and the rest fell into smaller categories. It will take us additional time to unpack the geometric thinking the students displayed during the think alouds, but we have begun to document the types of comparisons students made during think aloud interviews regarding the fictitious student methods to mathematics problems. When students were making comparisons between the characters, most often they were discussing differences between the characters (n=484), but they also noted similarities (n=267) and used both WEP characters’ strategies to verify a mathematical idea (n=5). In addition, regardless of whether students were pointing out a similarity or difference in the two strategies, students often referred directly to the method they were using to solve a problem.
Specifically, when pointing out differences, students most often described differences in the methods the characters used to solve a problem (n=380). For example, when analyzing strategies related to translating a figure, one student stated, “Jaxon is more plotting it out, while Maxine is subtracting the values to go left or down. They both had it in the same spot, which is good; I think that’s the idea.” This student realized Jackson is using a visual geometric method, while Maxine is using an algebraic approach, yet they arrive at the same answer. This student was attending to the visual/algebraic aspects of Jaxon and Maxine’s approaches. Students noted differences in the students’ methods regarding WEP specific content. For example, in a WEP designed to have students understand why the interior angle sum in a triangle is 180 degrees, one student said, “Alex, like, ripped his triangle apart and… what did Morgan do? … Morgan, just drew the line and just used, like, the parallel cut by transversal stuff to figure everything out. To figure out that it was 180 degrees.” Here the student is attending to specific mathematics content in the WEP.
This research is the very beginning of showing a viable scientific basis for using comparisons to explore multiple solution strategies of students in geometry, as students were able to note similarities and differences in the strategies. Given critiquing reasoning is important to deepening mathematical understanding, these findings are a step towards documenting the ways in which contrasting cases can be used in geometry. Currently, we just completed our first classroom-based implementation of the materials, a randomized control experiment with 102 students engaging with the AC2inG materials. The main difference between the treatment and control groups was that the control group only engaged in one student solution at a time without the comparison page. An analysis of these data will be forthcoming after we have caught our breath from teaching middle school geometry for 14 days!
References
Krupa, E. E., Bentley, B., Mannix, J. P., & Star, J. R. (2019) Animated Contrasting Cases in Geometry: 8th Grade Supplemental Materials. Retrieved from: https://acinggeometry.org/
Opper, S. (1977). Piaget‘s clinical method. Journal of children’s Mathematical Behavior, 5, 90-107.
Piaget, J. (1976). The child’s conception of the world (J. Tomlinson and A. Tomlinson, Trans.). Littlefield, Adams & Co. (1926).Star, J. R., Pollack, C., Durkin, K., Rittle-Johnson, B., Lynch, K., Newton, K., & Gogolen, C. (2015). Learning from comparison in algebra. Contemporary Educational Psychology, 40, 41-54.
Suggested Citation
Krupa, E. (2022, May). Transformation of AC2inG Classroom-Based Research Due to COVID-19. GeT: The News!, 3(3). https://www.gripumich.org/v3-i3-sp2022/#transformation-of-ac2ing-classroom-based-research-due-to-covid-19

Teaching GeT Working Group Update
by Nathaniel Miller
The Teaching GeT working group continues to stay very busy. We are putting the final touches on what will be our first public version of the Student Learning Objectives (SLOs) for GeT courses. Once they are complete some time within the next month, they will go up on the website which we are in the process of finishing. Executive summaries of the SLOs will be published in our newly accepted chapter in the AMTE Professional Book Series, Vol. 5: Reflection on Past, Present and Future: Paving the Way for the Future of Mathematics Teacher Education. Once the SLOs are up on the website, we will continue to develop supporting materials, and would invite anyone who is interested in contributing to join us.
Suggested Citation
Miller, N. (2022, May). The Teaching GeT Working Group Update Spring 2022. GeT: The News!, 3(3). https://www.gripumich.org/v3-i3-sp2022/#teaching-get-working-group-update

GeT Course Student Learning Outcome #2
by Teaching GeT Working Group Members
Evaluate geometric arguments and approaches to solving problems.
Geometry courses provide a natural setting for students to reflect on their reasoning, share their reasoning, and then critique the reasoning of their peers. If students only ever see correct arguments given by teachers and textbooks, they may not learn how to critically evaluate arguments. The ability to evaluate other people’s arguments is an important real-world skill that is related to, but separate from, the skill of proof writing.
Critiquing reasoning is a competency that needs to be practiced in order to improve and is an essential skill for future geometry teachers. Students should have opportunities to critique reasoning throughout a geometry course. This can take on many forms–critiquing their own or other students’ proofs, working together in groups to solve a problem, classroom discussions of problems or proofs, posing problems that lead to student disagreement, and learning about the geometric thought process in the Van Hiele Levels.
Providing opportunities for students to critique geometric reasoning is also important for understanding nuances in geometric definitions [see SLO 5] and in geometric notation. An essential opportunity for students to practice critiquing reasoning is when GeT students present their reasoning and proofs to the class, with the instructor modeling and moderating positive and negative feedback and depth of questioning. Some instructors have also found it valuable to introduce others’ arguments that could arise in high school geometry contexts, such as sample student proofs or video approximations of secondary teaching situations. Instructors can position GeT students in the role of a teacher, rather than another student, and invite broad and diverse observations about “students’” thinking. These discussions allow GeT students to practice critiquing reasoning while simultaneously deepening their understanding of secondary geometry content [see SLO 3].
While some of this reasoning will be in the form of formal proofs, other reasoning will be much more informal. Class discussions and solving problems in groups can be great opportunities for students to practice critiquing the work of others. If groups are solving non-routine problems together, there are bound to be many opportunities for students to discuss their reasoning and to listen to and evaluate the reasoning of their peers. Likewise, whole-class discussions are further opportunities for students to hear and evaluate the reasoning of their peers. In an inquiry-based geometry classroom, one of the goals of the instructor is likely to be to create an environment in which students feel supported in sharing their reasoning and their thoughts about other people’s reasoning in a supportive way.
If a classroom environment is achieved in which people feel safe to share their reasoning and their thoughts about other people’s positions, then genuine disagreements may arise in the class. When this happens, this can be one of the situations that is most conducive to deep learning. When students feel that they have an emotional stake in the outcome of a discussion, they start paying deep attention to arguments on both sides. Instructors can look for problems to pose that are likely to lead good students to disagreements. Non-Euclidean geometries [see SLO 9] are particularly fertile for leading to productive disagreements, as everything there will be new and unfamiliar, and it will take some time to reach an agreement as to how to proceed. For example, students can try to decide which of Euclid’s Postulates and/or Propositions [see SLO 7] are true in a new geometry or what familiar definitions [see SLO 6] give rise to in other geometries. Any situation where students are making conjectures and trying to evaluate if they are true will lead to opportunities for students to come up with competing ideas that they will need to resolve.
Interestingly, GeT instructors anecdotally have reported that a growing number of college students are exhibiting gaps in their geometric understandings and convey that students in their college classrooms sometimes struggle with visualizing relationships among quadrilaterals and have difficulties characterizing them. The Van Hiele levels are levels of learners’ geometric thinking and understanding (Mason, 1998). The five sequential levels include Visualization, Analysis, Abstraction, Deduction, and Rigor. This model of geometric learning posits that students at all levels will move through these different levels each time they encounter a new geometric subject. Although we expect preservice teachers to reach a high geometric thinking level (level 4 or 5), students who enter a high school geometry class typically perform at the lower levels. Therefore, it is recommended that GeT instructors create opportunities for preservice teachers to critique reasoning at various thinking levels. While it is natural for group activities to provide opportunities for the analysis of reasoning, the use of individual assignments can also be useful. For example, the use of end-of-class self-reflection assignments can provide GeT instructors feedback regarding gaps in student understanding or provide evidence of creative thinking and insightful connections.
Some other ways that instructors have implemented this standard in their classrooms include:
- Grading mock proofs on a test;
- Having students create rubrics for an assignment and evaluate their own work;
- Looking at possible K12 classroom activities and asking students to critique them and to discuss them in reference to their own future teaching; and
- Doing a jigsaw, pair/share, or speed dating activities discussing proof.
Regardless of the form that critiquing takes, it is an essential aspect of a GeT course as it helps students think critically, improve their reasoning skills, learn how to develop solid mathematical arguments, and become better mathematicians.
References
Mason, M. (1998). The Van Hiele levels of geometric understanding. In L. McDougal (Ed.) The professional handbook for teachers: Geometry (pp. 4-8). McDougal-Littell/Houghton-Mifflin.
Suggested Citation
An, T., Boyce, S., Cohen, S., Escuadro, H., Krupa, E., Miller, N., Pyzdrowski, L., Szydlik, S., & Vestal, S. (2022, May). GeT Course Student Learning Outcome #2. GeT: The News!, 3(3). https://www.gripumich.org/v3-i3-sp2022/#get-course-student-learning-outcome-2

Transformations Working Group Update
by Julia St. Goar
In the spring of 2022, the transformation geometry working group advanced several of its on-going goals. One of the major goals of the past year has been collecting and creating activities and sequences of activities that contribute to student understanding of the topic of transformations. In the spring of 2021, the working group created a lesson that engaged students in an activity focused on the creation of mathematical definitions in a transformation context (Boyce et. al., 2021); this semester members of the working group presented on and retaught the lesson. Additionally, the working group continued its exploration of existing transformation teaching materials.
This spring, in 2022, several members of the transformation group collaborated on and completed the following presentations on the lesson study (Boyce et. al., 2021):
- a GeT: a Pencil seminar on January 21st titled “Engaging Prospective Teachers in Defining Mutuality” by Steven Boyce, Laura Pyzdrowski, Ruthmae Sears, and Julia St. Goar;
- a presentation with the same title at the AMTE conference on February 10 by presenters Steven Boyce and Laura Pyzdrowski; and
- a presentation at the RUME conference on February 24 about the lesson study by Steven Boyce, Mike Ion, Ruthmae Sears, and Julia St. Goar within the context of the GeT: a Pencil working group, Improving Teaching and Learning in Undergraduate Geometry Courses for Secondary Teachers.
On April 14 of this year, Steven Boyce remotely re-taught the lesson in Matthew Shraeder’s class at West Virginia University, while several other members of the transformation group attended remotely. The transformation group discussed the outcomes of this iteration of the lesson and is currently considering new options moving forward with this lesson to make it a better fit for different types of GeT courses and to further deepen some of the lesson content.
Additionally, this semester the transformation group decided to focus on considering several different sets of existing course materials involving transformational geometry. This is a continuation of previous work considering course materials from sources like those by Douglas and Picciotto (2017). This semester, two different members of the transformation group, Priya Prasad and Yvonne Lai, volunteered their course materials related to transformation geometry for the purposes of discussion in the working group. Additionally, the group began discussing some of the materials on transformation geometry produced by MODULES(S2) (Alibegovic et. al., n.d.). In each case, one to two full meetings were devoted to each set of materials. Focuses of the discussions included a.) working to understand the teaching goals of each set of materials under discussion, as well as b.) (when applicable) considering the definitions and possible axiomatic structure used by the materials for both their mathematical accuracy and appropriateness in an undergraduate or high school setting. This second point of discussion relates to the transformation group’s ongoing interest in axiomatic systems based on transformations. These meetings on existing course materials were especially fruitful and, due to the large amount of content present in several of these sets of materials, will likely be the source of future ongoing discussion within the working group.
References
Alibegovic, E., Anhalt, C., Aubrey, J., Casey, S., Cortez, R., Czap, L., Gobstein, H., Hart, J., Kohler, B., Lai, Y., Lischka, A., Maddox, S., Patterson, C., Ross, A., Strayer, J., Tuttle, J., & Weiss, M. (n.d.) Our Project. MODULES(S2): Mathematics of Doing, Understanding, Learning and Education for Secondary Schools. https://modules2.com/our-project/
Boyce, S., Ion, M., Lai, Y., McLeod, K., Pyzdrowski, L., Sears, R., & St. Goar, J. (2021, May 6). Best-Laid Co-Plans for a Lesson on Creating a Mathematical Definition. AMS Blogs: On Teaching and Learning Mathematics. https://blogs.ams.org/matheducation/2021/05/06/best-laid-co-plans-for-a-lesson-on-creating-a-mathematical-definition/
Douglas, L. & Picciotto, H. (August, 2017). Transformational proof in high school geometry: A guide for teachers and curriculum developers. Retrieved from https://www.mathedpage.org/transformations/proof/transformational-proof.pdf.
Suggested Citation
St. Goar, J. (2022, May). The Transformations Working Group Update Spring 2022. GeT: The News!, 3(3). https://www.gripumich.org/v3-i3-sp2022/#transformations-working-group-update

GeT to Know the Community
Four questions with Dorin Dumitrascu, Associate Professor of Mathematics at Adrian College
- What is special about your GeT course? In 2-3 sentences, describe your GeT course.
My course is an axiomatic exploration of two-dimensional Euclidean geometry. I try to keep a balance between mathematical precision in exposition and allowing students to discover and share their study of shapes with their peers. This balancing act happens because I know that the students need to see in class concrete examples of how to approach, solve, explain, and write solutions to problems, but I am also an inquiry-based practitioner. I believe that they should work on their own understanding of the subject. The focus of my course is on communication, both written and oral. I also like GeoGebra very much, and I use technology in the exploration process.
- Who are your students?
At Adrian College, Geometry is one of the core courses for secondary and elementary teacher education math majors and is an elective for the pure mathematics major and minor. Consequently, about two thirds of the students are pre-service teachers, with occasional physics and chemistry students taking it out of intellectual curiosity. One of the goals of the course is to train the students in becoming better writers and readers of mathematical proofs.
- What are you most interested in learning/achieving through participating with the GeT: A Pencil community?
I initially joined the group because I wanted to share my experience teaching the course and learn the approaches of other people across the country. I am grateful for everything that people presented and discussed in the working groups and during other meetings that we had since that first 2018 conference in Ann Arbor.
- What is your favorite book you have read in the last few years?
The most interesting book that I read recently is Joe Dispenza’s Breaking the Habit of Being Yourself. As I try to deepen my understanding of quantum physics, I find fascinating the attempt to connect spirituality, neuroscience, and the quantum aspect of the universe.

Did you get promoted? Win a grant? Have a baby? Buy a house? We would love to feature your news, whether professional or personal! Email us at GRIP@umich.edu.

Member News

Julia St. Goar, Associate Professor of Mathematics, Merrimack College, received tenure and was promoted to Associate Professor of Mathematics.

Erin Krupa, Assistant Professor of Science, Technology, Engineering, and Mathematics Education, North Carolina State University, has received tenure and has been promoted to Associate Professor, effective August 15, 2022.

Upcoming Event
GeT: A Pencil Community Meeting
This year’s GeT: A Pencil Community Meeting will take place on Friday, June 10 at 2:00 PM ET. During this 90-min Zoom meeting, we will look back at what we have accomplished together this past year and discuss future plans.
Please let us know if you are or are not able to attend by responding to this quick survey

To submit a paper to be highlighted in a future newsletter, please fill out this form.
GeT Support
Sponsored by NSF DUE-1725837. All opinions are those of the authors and do not necessarily represent the views of the National Science Foundation or the University of Michigan.
Patricio Herbst, PI
Amanda Milewski, Co-PI
Get Support is housed in the GRIP Lab at the University of Michigan
Inese Berzina Pitcher, Project Manager
